
分析 (1)由条件利用三角函数的恒等变换,化简函数f(x)的解析式,再根据函数的零点的定义求得(x)的正零点.
(2)由条件利用累加法求数列{bn}的通项公式.
解答 解:(1)f(x)=$\sqrt{3}$sinπx-sin(πx+$\frac{π}{6}$)=$\sqrt{3}$sinπx-sinπxcos$\frac{π}{6}$-cosπxsin$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$sinπx-$\frac{1}{2}$cosπx=sin(πx-$\frac{π}{6}$),
令f(x)=sin(πx-$\frac{π}{6}$)=0,求得 πx-$\frac{π}{6}$=kπ,k∈N,即 x=k+$\frac{1}{6}$,k∈N.
(2)f(x)的所有正零点依次组成数列{an},则an=n-$\frac{5}{6}$,
数列{bn}满足b1=0,bn+1-bn=an,n∈N*,∴b1=0,b2-b1=1-$\frac{5}{6}$,b3-b2=2-$\frac{5}{6}$,…bn-bn-1=(n-1)-$\frac{5}{6}$,
累加可得 bn=0+(1-$\frac{5}{6}$)+(2-$\frac{5}{6}$)+…+(n-1-$\frac{5}{6}$)=[1+2+3+…+(n-1)]-(n-1)$\frac{5}{6}$=$\frac{(n-1)•n}{2}$-(n-1)$\frac{5}{6}$=$\frac{{3n}^{2}-8n-5}{6}$,
即bn=$\frac{{3n}^{2}-8n-5}{6}$.
点评 本题主要考查三角函数的恒等变换,函数的零点的定义,用累加法求数列的通项公式,属于中档题.


 新课标同步训练系列答案
新课标同步训练系列答案科目:高中数学 来源: 题型:解答题
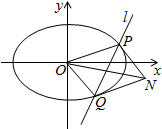 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | $\frac{{\sqrt{7}}}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
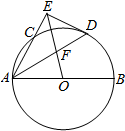 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com