
【题目】已知圆锥的侧面展开图是一个半圆.

(1)求圆锥的母线与底面所成的角;
(2)过底面中心![]() 且平行于母线
且平行于母线![]() 的截平面,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为
的截平面,若截面与圆锥侧面的交线是焦参数(焦点到准线的距离)为![]() 的抛物线,求圆锥的全面积;
的抛物线,求圆锥的全面积;
(3)过底面点![]() 作垂直且于母线
作垂直且于母线![]() 的截面,若截面与圆锥侧面的交线是长轴为
的截面,若截面与圆锥侧面的交线是长轴为![]() 的椭圆,求椭圆的面积(椭圆号
的椭圆,求椭圆的面积(椭圆号![]() 的面积
的面积![]() )
)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据侧面展开图的特征列方程得出底面半径和母线的关系,从而得出母线和底面所成的角;
(2)根据抛物线的一条弦为圆锥底面直径得出底面半径和![]() 的关系,从而可得圆锥的面积;
的关系,从而可得圆锥的面积;
(3)根据三角形相似和圆锥的特点得出椭圆的长轴,短轴和底面半径的关系,从而可得长短轴的关系,得出答案.
(1)设圆锥的底面半径为![]() ,母线长为
,母线长为![]() ,则圆锥侧面展开图的半径为
,则圆锥侧面展开图的半径为![]() ,弧长为
,弧长为![]() ,
,
![]() 圆锥的侧面展开图是一个半圆,
圆锥的侧面展开图是一个半圆,
![]() ,
,![]() ,
,
![]() 圆锥的轴截面为等边三角形,
圆锥的轴截面为等边三角形,
![]() 圆锥的母线与底面所成的角为
圆锥的母线与底面所成的角为![]() ;
;
(2)设抛物线的顶点为![]() ,
,
![]() 截面
截面![]() ,
,![]()
则![]() 为
为![]() 的中点,
的中点,
设抛物线方程为![]() ,把
,把![]() 代入抛物线方程得
代入抛物线方程得![]() ,
,
![]() ,于是母线
,于是母线![]() ,
,
又由(1)可知![]() ,即
,即![]() ,
,![]() ,
,
![]() 圆锥的全面积为
圆锥的全面积为![]() ;
;
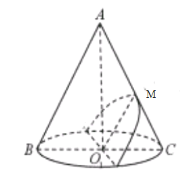
(3)设![]() 的中点为
的中点为![]() ,则
,则![]() 和
和![]() 为椭圆的长轴顶点,
为椭圆的长轴顶点,
取![]() 的中点
的中点![]() ,则
,则![]() 为椭圆的中心,连接
为椭圆的中心,连接![]() 并延长,交
并延长,交![]() 于
于![]() ,过
,过![]() 作
作![]() ,交圆锥底面圆周于
,交圆锥底面圆周于![]() ,
,
则![]() ,即
,即![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,由
,由![]() 可知
可知![]() ,又
,又![]() ,
,
![]() 为
为![]() 靠近
靠近![]() 的三等分点,连接
的三等分点,连接![]() ,
,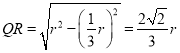 ,
,
![]() 中,根据余弦定理
中,根据余弦定理![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]() 中,过点
中,过点![]() 平行于
平行于![]() 的线段是
的线段是![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,
所以椭圆面积![]()


科目:高中数学 来源: 题型:
【题目】设P是椭圆![]() 上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
上一点,M,N分别是两圆(x+4)2+y2=1和(x-4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值分别为 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,直线
,直线![]() 恰好经过椭圆C:
恰好经过椭圆C:![]() 的右顶点和上顶点.
的右顶点和上顶点.
(1)求椭圆C方程;
(2)过椭圆C左焦点F的直线l交椭圆C于![]() 两点,椭圆上存在一点P,使得四边形
两点,椭圆上存在一点P,使得四边形![]() 为平行四边形,求直线l的方程。
为平行四边形,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
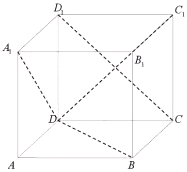
【题目】如图,![]() 的棱长为1的正方体,任作平面
的棱长为1的正方体,任作平面![]() 与对角线
与对角线![]() 垂直,使得
垂直,使得![]() 与正方体的每个面都有公共点,这样得到的截面多边形的面积为
与正方体的每个面都有公共点,这样得到的截面多边形的面积为![]() ,周长为
,周长为![]() 的范围分别是_____________(用集合表示)
的范围分别是_____________(用集合表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( ).
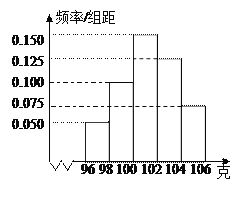
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乳业公司生产甲、乙两种产品,需要A,B,C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如下表所示:
产品 苜蓿草饲料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,已知生产1个单位甲产品,产生的利润为2万元;生产1个单位乙产品,产生的利润为3万元,分别用x,y表示生产甲、乙两种产品的数量.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中,原文记载如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”其核心思想编译成如示框图,若输入的![]() ,
,![]() 分别为45,63,则输出的
分别为45,63,则输出的![]() 为( )
为( )
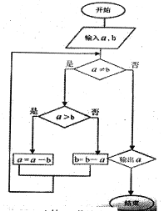
A. 2B. 3C. 5D. 9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com