
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]() .
.
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)由(1)写出数列{bn}的前n项和Sn , 并用数学归纳法证明.
【答案】
(1)解:∵a1=2,an+1= ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
又bn=| ![]() |,得b1=4,b2=8,b3=16,
|,得b1=4,b2=8,b3=16,
猜想: ![]()
(2)解:由(1)可得,数列{bn}是以4为首项,2为公比的等比数列,
则有 ![]() .
.
证明:当n=1时, ![]() 成立;
成立;
假设当n=k时,有 ![]() ,
,
则当n=k+1时, ![]() =2k+3﹣4=2(k+1)+2﹣4.
=2k+3﹣4=2(k+1)+2﹣4.
综上, ![]() 成立
成立
【解析】(1)由已知结合数列递推式求得b1 , b2 , b3 , 并猜想bn的表达式;(2)由等比数列的前n项和公式求得数列{bn}的前n项和Sn , 并用数学归纳法证明.
【考点精析】关于本题考查的数列的前n项和和数学归纳法的定义,需要了解数列{an}的前n项和sn与通项an的关系 ;数学归纳法是证明关于正整数n的命题的一种方法才能得出正确答案.
;数学归纳法是证明关于正整数n的命题的一种方法才能得出正确答案.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1 , F是棱DD1与平面BEP的交点,则DF的长为( ) 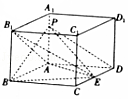
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
用煤(吨) | 用电(千瓦) | 产值(万元) | |
甲产品 | 3 | 50 | 12 |
乙产品 | 7 | 20 | 8 |
但国家每天分配给该厂的煤、电有限,每天供煤至多47吨,供电至多300千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业投资1千万元用于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.经过多少年后,该项目的资金可以达到4倍的目标?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=1,Sn+1﹣2Sn=1(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=n+ ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=2sin( ![]() )(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(
)(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则( ![]() +
+ ![]() )
) ![]() =( )
=( )
A.﹣32
B.﹣16
C.16
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都是正数,且对任意n∈N* , 都有(an﹣1)(an+3)=4Sn , 其中Sn为数列{an}的前n项和.
(1)求证数列{an}是等差数列;
(2)若数列{ ![]() }的前n项和为Tn , 求Tn .
}的前n项和为Tn , 求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com