
【题目】为了更好地支持“中小型企业”的发展,某市决定对部分企业的税收进行适当的减免,某机构调查了当地的中小型企业年收入情况,并根据所得数据画出了样本的频率分布直方图,下面三个结论:

①样本数据落在区间![]() 的频率为0.45;
的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受减免税政策,估计有55%的当地中小型企业能享受到减免税政策;
③样本的中位数为480万元.
其中正确结论的个数为( )
A.0B.1C.2D.3
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,
,![]() ,M是椭圆E上的一个动点,且
,M是椭圆E上的一个动点,且![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆E的标准方程,
(2)若![]() ,
,![]() ,四边形ABCD内接于椭圆E,
,四边形ABCD内接于椭圆E,![]() ,记直线AD,BC的斜率分别为
,记直线AD,BC的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网购已逐渐融入了人们的生活.网购是非常方便的购物方式,为了了解网购在某市的普及情况,某调查机构进行了有关网购的调查,并从参与调查的市民中随机抽取了男、女各100人进行分析,得到如下所示的统计表.
经常网购 | 偶尔网购或不网购 | 合计 | |
男性 | 50 | 100 | |
女性 | 70 | 100 | |
合计 |
附: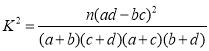 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)完成上表,并根据以上数据判断能否在犯错误的概率不超过0.01的前提下认为该市市民的网购情况与性别无关.
(2)①现从所抽取的100位女性市民中利用分层抽样的方法抽取10人,再从这10人中随机选取3人赠送优惠券,求选取的3人中至少有2人经常网购的概率;
②将频率视为概率,从该市所有参与调查的市民中随机抽取10人赠送礼品,记其中经常网购的人数为X,求随机变量X的数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,则a= ( )
sin A,则a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根据正弦定理把![]() 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
根据正弦定理,![]() 可化为
可化为![]()
∵△ABC的周长为![]() ,
,
∴联立方程组![]() ,
,
解得a=2.
故选:B
【点睛】
(1)在三角形中根据已知条件求未知的边或角时,要灵活选择正弦、余弦定理进行边角之间的转化,以达到求解的目的.
(2)求角的大小时,在得到角的某一个三角函数值后,还要根据角的范围才能确定角的大小,这点容易被忽视,解题时要注意.
【题型】单选题
【结束】
7
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
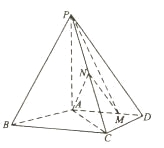
(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说,年过半百的笛卡尔担任瑞典一小公国的公主克里斯蒂娜的数学老师,日久生情,彼此爱慕,其父国王知情后大怒,将笛卡尔流放回法国,并软禁公主,笛卡尔回法国后染上黑死病,连连给公主写信,死前最后一封信只有一个公式:![]()
![]() 国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系
国王不懂,将这封信交给了公主,公主用笛卡尔教她的坐标知识,画出了这个图形“心形线”.明白了笛卡尔的心意,登上了国王宝座后,派人去寻笛卡尔,其逝久矣(仅是一个传说).心形线是由一个圆上的一个定点,当该圆绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名.在极坐标系![]() 中,方程
中,方程![]()
![]() 表示的曲线
表示的曲线![]() 就是一条心形线,如图,以极轴
就是一条心形线,如图,以极轴![]() 所在直线为
所在直线为![]() 轴,极点
轴,极点![]() 为坐标原点的直角坐标系
为坐标原点的直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为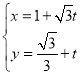 (
(![]() 为参数).
为参数).
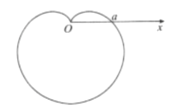
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若曲线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 、
、![]() 三点,求线段
三点,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在坐标原点
的顶点在坐标原点![]() ,对称轴为
,对称轴为![]() 轴,焦点为
轴,焦点为![]() ,抛物线上一点
,抛物线上一点![]() 的横坐标为2,且
的横坐标为2,且![]() .
.
(1)求抛物线的方程;
(2)过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为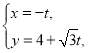 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线和曲线
分别交直线和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com