
【题目】在直三棱柱ABC﹣A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a. 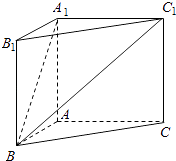
(1)求a的值;
(2)求平面A1BC1与平面B1BC1所成的锐二面角的大小.
【答案】
(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,
即∠A1BC=60°,(2分)
连接A1C,又AB=AC,则A1B=A1C∴△A1BC为等边三角形,
由AB=AC=1,∠BAC=90° ![]() ,
,
∴ ![]()
(2)解:取A1B的中点E,连接B1E,过E作EF⊥BC1于F,
连接B1F,B1E⊥A1B,A1C1⊥B1EB1E⊥平面A1BC1B1E⊥BC1
又EF⊥BC1,所以BC1⊥平面B1EF,即B1F⊥BC1,
所以∠B1FE就是平面A1BC1与平面B1BC1所成的锐二面角的平面角.
在△B1EF中,∠B1EF=90°, ![]() ,
, ![]() ,∴
,∴ ![]() ∠B1FE=60°,
∠B1FE=60°,
因此平面A1BC1与平面B1BC1所成的锐二面角的大小为60°.
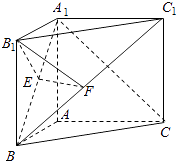
【解析】(1)将B1C1平移到BC,∠A1BC就是异面直线A1B与B1C1所成的角,在三角形A1BA内建立等式,解之即可;(2)取A1B的中点E,连接B1E,过E作EF⊥BC1于F,连接B1F,B1E⊥A1B,A1C1⊥B1E,得到∠B1FE就是平面A1BC1与平面B1BC1所成的锐二面角的平面角,在△B1EF中解出此角即可.
【考点精析】本题主要考查了平面与平面之间的位置关系的相关知识点,需要掌握两个平面平行没有交点;两个平面相交有一条公共直线才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4[sin(θ+ ![]() )]x﹣2,θ∈[0,2π]].
)]x﹣2,θ∈[0,2π]].
(1)若函数f(x)为偶函数,求tanθ的值;
(2)若f(x)在[﹣ ![]() ,1]上是单调函数,求θ的取值范围.
,1]上是单调函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 3 | 4 | 8 | 15 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 15 | x | 3 | 2 |
乙校:
分组 | [70,80) | [80,90) | [90,100) | [100,110) |
频数 | 1 | 2 | 8 | 9 |
分组 | [110,120) | [120,130) | [130,140) | [140,150] |
频数 | 10 | 10 | y | 3 |
则x,y的值分别为( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得 M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=m. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=﹣ ![]() x3+
x3+ ![]() x2+2ax.
x2+2ax.
(1)当a=1时,求f(x)在[1,4]上的最大值和最小值.
(2)若f (x)在( ![]() ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com