
(理科题)(本小题12分)
已知数列{an}是等差数列,a2=3,a5=6,数列{bn}的前n项和是Tn,且Tn+ bn=1.
bn=1.
(1)求数列{an}的通项公式与前n项的和 ;
;
(2)求数列{bn}的通项公式.
(1)∴an=2+(n-1)=n+1.Sn=na1+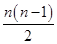 d=
d=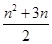 .
(2)证明:见解析。
.
(2)证明:见解析。
【解析】
试题分析:(1)设{an}的公差为d,进而根据等差数列通项公式表示出a2和a5,求得a1和d,则数列的通项公式和求和公式可得.
(2)根据Tn-Tn-1=bn,整理得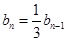 ,判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案..
,判断出{bn}是等比数列.进而求得b1,利用等比数列的通项公式求得答案..
(1)设{an}的公差为d,则:a2=a1+d,a5=a1+4d.
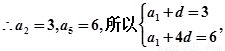 ……………2分
……………2分
∴a1=2,d=1 ……………3分
∴an=2+(n-1)=n+1.…………4分
Sn=na1+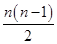 d=
d=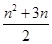 .………………6分
.………………6分
(2)证明:当n=1时,b1=T1,
由T1+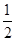 b1=1,得b1=
b1=1,得b1=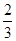 .
………8分
.
………8分
当n≥2时,∵Tn=1-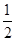 bn,Tn-1=1-
bn,Tn-1=1-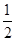 bn-1,
bn-1,
∴Tn-Tn-1=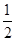 (bn-1-bn),……………10分
(bn-1-bn),……………10分
即bn=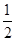 (bn-1-bn).
(bn-1-bn).
∴bn=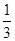 bn-1. …………11分
bn-1. …………11分
∴{bn}是以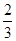 为首项,
为首项,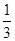 为公比的等比数列.∴bn=
为公比的等比数列.∴bn=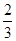 ·(
·(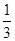 )n-1=
)n-1=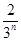 .……………12分
.……………12分
考点:等差数列的通项公式;考查了等差数列的性质和等比数列的判定,等差数列的前n项和;等比数列的通项公式.
点评:先求出等差数列的前n项和Sn,然后就可以求出Tn,再利用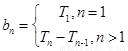 可求{bn}
可求{bn}
的通项公式。


科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
定义在区间(0,![]() )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有![]() .
.
(1)求证:方程f(x)=0有且只有一个实根;
(2)若a>b>c>1,且a、b、c成等差数列,求证:![]() ;
;
(3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省南京六中高二下学期期中考试理数 题型:解答题
(本小题满分15分)在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题.求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到文科题的概率
查看答案和解析>>
科目:高中数学 来源:2014届福建福州文博中学高二上学期期中考试数学试卷(解析版) 题型:解答题
(理科题)(本小题12分)
某房产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。
(1)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(2)若干年后开发商为了投资其他项目,有两种处理方案①年平均利润最大时以46万元出售该楼;
②纯利润总和最大时,以10万元出售楼,问选择哪种方案盈利更多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com