
【题目】已知直线![]() 、
、![]() 、
、![]() 两两成异面直线.问是否存在直线
两两成异面直线.问是否存在直线![]() 同时与
同时与![]() 、
、![]() 、
、![]() 相交?证明你的结论.
相交?证明你的结论.
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽子3个,肉粽子2个,白粽子5个,这三种粽子的外观完全相同,从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设ξ表示取到的豆沙粽子个数,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与定直线
,且与定直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的任一条直线
的任一条直线![]() 与轨迹
与轨迹![]() 交于不同的两点
交于不同的两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,将函数
,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后,得到函数
个单位长度后,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的表达式;
的表达式;
(2)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)若函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村充分利用自身资源,大力发展养殖业以增加收入.计划共投入80万元,全部用于甲、乙两个项目,要求每个项目至少要投入20万元在对市场进行调研时发现甲项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足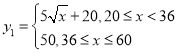 ,乙项目的收益
,乙项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足![]() .
.
(1)当甲项日的投入为25万元时,求甲、乙两个项目的总收益;
(2)问甲、乙两个项目各投入多少万元时,总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com