
����Ŀ��ij�е���̨Ϊ���������ٰ��ʴ�������Ը���15��65�����Ⱥ���г�����Ƶ�ʷֲ�ֱ��ͼ���ش�����ͳ�ƽ�������ʾ��
��� | ���� | �ش���ȷ | �ش���ȷ������ |
��1�� | [15��25�� | 5 | 0.5 |
��2�� | [25��35�� | a | 0.9 |
��3�� | [35��45�� | 27 | x |
��4�� | [45��55�� | b | 0.36 |
��5�� | [55��65�� | 3 | y |
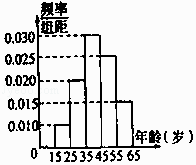
��1���ֱ����a��b��x��y��ֵ��
��2���ӵ�2��3��4��ش���ȷ�������÷ֲ�����ķ�����ȡ6�ˣ����2��3��4��ÿ��Ӧ����ȡ�����ˣ�
��3���ڣ�2����ǰ���£�����̨����������ȡ��6���������ȡ3�˰䷢���˽���������ȡ�����е�3��������1�˻�����˽��ĸ��ʣ�
���𰸡�
��1���⣺��1������5��0.05=100��
����n=100��0.1=1000��
��2������1000��0.2=200������a=200��0.9=180��
��3������1000��0.3=300������x=270��300=0.9��
��4������1000��0.25=250������b=250��0.36=90��
��5������1000��0.15=150������y=3��150=0.02
��2���⣺��2��3��4��ش���ȷ���˵ı�Ϊ180��270��90=2��3��1��
�ӵ�2��3��4��ش���ȷ�������÷ֲ�����ķ�����ȡ6�ˣ�
���Ե�2��3��4��ÿ��Ӧ�����γ�ȡ2�ˣ�3�ˣ�1��
��3���⣺�dz�ȡ��6���У���2��ļ�Ϊa1��a2����3��ļ�Ϊb1��b2��b3����4��ļ�Ϊc��
���6��ѧ������ȡ3�������п��ܵ������20�֣������ǣ� 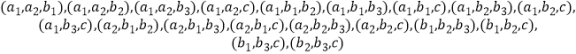
���мǡ���3��������1�ˡ�Ϊ�¼�A����A�Ķ����¼��ǡ���3���û��ѡ������
������¼�������1��������a1��a2��c����
������ȡ�����е�3��������1�˻�����˽��ĸ���Ϊ ![]()
����������1���������1������Ϊ100���Ӷ��õ�n=1000���ɴ���������a��b��x��y��ֵ����2����2��3��4��ش���ȷ���˵ı�Ϊ2��3��1���ɴ��������2��3��4��ÿ��Ӧ����ȡ����������3���dz�ȡ��6���У���2��ļ�Ϊa1 �� a2 �� ��3��ļ�Ϊb1 �� b2 �� b3 �� ��4��ļ�Ϊc���ɴ������оٷ����������ȡ�����е�3��������1�˻�����˽��ĸ��ʣ�
�����㾫����������Ҫ������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ�㣬��Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�Ľ�A��B��C���Եı߷ֱ�Ϊa��b��c���� ![]() �� �������A�Ĵ�С��
�� �������A�Ĵ�С��
������a=1�� ![]() ����b+c��ֵ��
����b+c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B��C��Բx2+y2=1���˶�����AB��BC������P������Ϊ ![]() ����
���� ![]() ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��
A.[8��10]
B.[9��11]
C.[8��11]
D.[9��12]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�У�PA��ƽ��ABCD������ABCD�DZ߳�Ϊ2�������Σ�PA=AD��FΪPD���е㣮 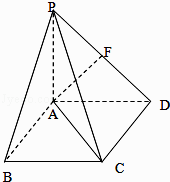
��1����֤��AF��ƽ��PDC��
��2����ֱ��AC��ƽ��PCD���ɽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() �����ҽ���ֱ�ΪF1 �� F2 �� ��F2Ϊ������
�����ҽ���ֱ�ΪF1 �� F2 �� ��F2Ϊ������ ![]() �Ľ��㣬C2����l��C1��Բx2+y2=a2�صõ��ҳ��ֱ�Ϊ
�Ľ��㣬C2����l��C1��Բx2+y2=a2�صõ��ҳ��ֱ�Ϊ ![]() ��4��
��4��
��1����C1��C2�ķ��̣�
��2��ֱ��l1��F1����C2���ཻ��ֱ��l2��F2����l1ƽ�У���l1��C1��A��B��l2��C1����C��D������x���Ϸ������ı���AF1F2C�������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��ʾ����ֱ�ߣ������±�ʾ����ƽ�棬������������ȷ���� �� ����д������ȷ�������ţ� ����a��b��a�Φ�����b�Φ��� ����a��b��a����b�ͦ£�����ͦ£�
�������Φ£�a�ͦ�����a�ͦ£��������ͦ£�a��b��a�ͦ�����b�ͦ£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ����Ҫ����A��B�����߲�ÿ��ļ۸�ֱ�Ϊ2Ԫ��3Ԫ��������Ҫ��A���߲�����Ҫ��6�B���߲�����Ҫ��4�����һ���й����������߲˵��ܷ��ò��ܳ���60Ԫ�� 
��1��д��һ����A���߲˹��������x��B���߲˹��������y֮��IJ���ʽ�飻
��2�����������������ϵ�л�����1���в���ʽ���ʾ��ƽ����������Ӱ��ʾ������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABC��A1B1C1�У�CA=CB��M��N��P�ֱ�ΪAB��A1C1 �� BC���е㣮 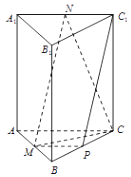
��֤��
��1��C1P��ƽ��MNC��
��2��ƽ��MNC��ƽ��ABB1A1 ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com