
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
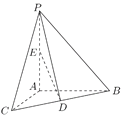
(1)求三棱锥![]() 的体积;
的体积;
(2)若异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)三棱锥P﹣ABC中,由PA⊥平面ABC,AC⊥AB,利用VP﹣ABC![]() PA能求出三棱锥P﹣ABC的体积.
PA能求出三棱锥P﹣ABC的体积.
(2)取AC中点F,连接DF,EF,则AB∥DF,得∠EDF(或其补角)就是异面直线AB与ED所成的角θ,由此能求出tanθ.
(1)三棱锥P﹣ABC中,
∵PA⊥平面ABC,AC⊥AB,AP=BC=4,∠ABC=30°,D、E分别是BC、AP的中点,
∴AC=2,AB=2![]() ,
,
所以,体积VP﹣ABC![]() PA
PA![]() .
.
(2)取AC中点F,连接DF,EF,则AB∥DF,
所以∠EDF(或其补角)就是异面直线AB与ED所成的角θ.
由已知,AC=EA=AD=2,AB=2![]() ,PC=2
,PC=2![]() ,
,
∵AB⊥EF,∴DF⊥EF.
在Rt△EFD中,DF![]() ,EF
,EF![]() ,
,
所以,tanθ![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
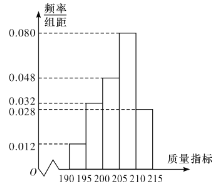
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与椭圆
与椭圆![]() 有一个相同的焦点,过点
有一个相同的焦点,过点![]() 且与
且与![]() 轴不垂直的直线
轴不垂直的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)试问直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为![]() ,再由乙猜甲刚才想的数字把乙猜的数字记为
,再由乙猜甲刚才想的数字把乙猜的数字记为![]() ,且
,且![]() ,若
,若![]() ,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com