
【题目】如果函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意
,对于定义域内的任意![]() 存在实数
存在实数![]() 使得
使得![]() 成立,则称此函数具有“
成立,则称此函数具有“![]() 性质”.
性质”.
(1)判断函数![]() 是否具有“
是否具有“![]() 性质”,若具有“
性质”,若具有“![]() 性质”,写出所有
性质”,写出所有![]() 的值;若不具有“
的值;若不具有“![]() 性质”,请说明理由.
性质”,请说明理由.
(2)设函数![]() 具有“
具有“![]() 性质”,且当
性质”,且当![]() 时,
时,![]() ,求当
,求当![]() 时函数
时函数![]() 的解析式;若
的解析式;若![]() 与
与![]()
![]() 交点个数为1001个,求
交点个数为1001个,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的为( )
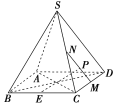
A.①③B.③④C.①②D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点 |
B.存在定点P不在M中的任一条直线上 |
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上 |
D.M中的直线所能围成的正三角形面积都相等 |
其中真命题的代号是 (写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员毎次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算机产生0到9之间取整数值的随机数,指定1,3,4表示命中,5,6,7,8,9,0表示不命中;再以三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
![]()
据此估计,该运动员三次投篮恰有两次命中的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,若
中,若![]() (
(![]() ,
,![]() ,p为常数),则称
,p为常数),则称![]() 为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
为“等方差数列”.下列是对“等方差数列”的判断,正确的是( )
A.![]() 不是等方差数列;
不是等方差数列;
B.若![]() 既是等方差数列,又是等差数列,则该数列为常数列;
既是等方差数列,又是等差数列,则该数列为常数列;
C.已知数列![]() 是等方差数列,则数列
是等方差数列,则数列![]() 是等方差数列;
是等方差数列;
D.若![]() 是等方差数列,则
是等方差数列,则![]() (
(![]() ,k为常数)也是等方差数列.
,k为常数)也是等方差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长沙某公司对其主推产品在过去5个月的月广告投入xi(百万元)和相应的销售额yi(百万元)进行了统计,其中i=1,2,3,4,5,对所得数据进行整理,绘制散点图并计算出一些统计量如下:

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,其中
,其中![]() ,i=1,2,3,4,5.
,i=1,2,3,4,5.
(Ⅰ)根据散点图判断,![]() 与
与![]() 哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为月销售额关于月广告投入xi的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及题中所给数据,建立y关于x的回归方程,并据此估计月广告投入220万元时的月销售额.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00-99编号,并且按编号顺序平均分成10组,现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
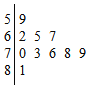
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩的茎叶图如图所示,这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的方程为(x-1)2+(y-1)2=9,P(2,2)是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com