
分析 通过数学归纳法证明即可.
解答 解:集合B中元素个数的最大值为n+1.
取B={1,3,5,…,2n+1},则此集合中任意两个数之和为偶数,符合题意.
下面证明取A中任何n+2个元素组成的集合B,一定有两个数之和仍然在B中.
用数学归纳法证明.
当n=1时,A={1,2,3},取A中3个元素的集合B={1,2,3},显然有1+2=3,结论成立.
假设n时结论成立,即A={1,2,3,…,2n,2n+1}中任意n+2个元素的集合B必有两个数之和仍在B中.
对于n+1时,A={1,2,3,…,2n+1,2n+2,2n+3},从A中任取n+3个元素组成集合B.
下面证明B中必有两个数之和仍在B中.
若所取的n+3个数不含有2n+2或2n+3,那么必在{1,2,3,…,2n,2n+1}中取出n+2个数.
由归纳假设,必有两个数之和在B中,结论成立.
对所取的n+3个数含有2n+2和2n+3,则要在{1,2,3,…,2n,2n+1}取出n+1数.
下面证明2n+3必可以表示成B中的两个数之和.
将1,2,3,…,2n+1,2n+2这2n+2个数分成n+1组(1,2n+2)、(2,2n+1)、(3,2n)、…、(n+1,n+2),
从中取出n+2个数中必有两个数在同一组.
由于2n+3=1+(2n+2)=2+(2n+1)=3+2n=…=(n+1)+(n+2),
故在1,2,3,…,2n,2n+1,2n+2所取的n+2必有两个数之和等于2n+3.
由数学归纳法原理可知集合A中任取n+2个数的集合B,在B中必有两数之和仍在B中.
因此,B中元素个数最大值为n+1.
点评 本题考查了集合问题,考查数学归纳法的证明,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.
平面α内有△ABC,AB=5,BC=8,AC=7,梯形BCDE的底DE=2,过EB的中点B1的平面β∥α,若β分别交EA、DC于A1、C1,求△A1B1C1的面积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
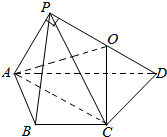 如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=2,PD=2$\sqrt{3}$,PA⊥PD,Q为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com