
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点是
的焦点是![]() ,准线是
,准线是![]() ,抛物线上任意一点
,抛物线上任意一点![]() 到
到![]() 轴的距离比到准线的距离少2.
轴的距离比到准线的距离少2.
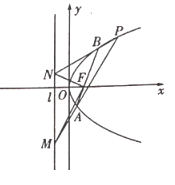
(1)写出焦点![]() 的坐标和准线
的坐标和准线![]() 的方程;
的方程;
(2)已知点![]() ,若过点
,若过点![]() 的直线交抛物线
的直线交抛物线![]() 于不同的两点
于不同的两点![]() (均与
(均与![]() 不重合),直线
不重合),直线![]() 分别交
分别交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,题目是:“今有池方一丈,点生其中央,出水一尺,引葭赶岸,适马岸齐,问水深,葭长各几何?”题意是:有一正方形池塘,边长为一丈(10尺),有棵芦苇长在它的正中央,高出水面部分有1尺长,把芦苇拉向岸边,恰好碰到沿岸(池塘一边的中点),则水深为__________尺,芦苇长__________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的30个零件编号为01,02,…,19,30,现利用如下随机数表从中抽取5个进行检测. 若从表中第1行第5列的数字开始,从左往右依次读取数字,则抽取的第5个零件编号为( )
34 57 07 86 36 04 68 96 08 23 23 45 78 89 07 84 42 12 53 31 25 30 07 32 86 |
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆O:x2+y2=4上一动点,过点A作AB⊥x轴,垂足为B,动点D满足![]() .
.
(1)求动点D的轨迹C的方程;
(2)垂直于x轴的直线M交轨迹C于M、N两点,点P(3,0),直线PM与轨迹C的另一个交点为Q.问:直线NQ是否过一定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到定直线
到定直线![]() 的距离小
的距离小![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,
,![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() .设线段
.设线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)在(2)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为![]() (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)直线l与曲线C交于AB两点,P(1,3),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com