分析:根据题中的数量积为零可得PA、PB、PC两两互相垂直,从而以PA、PB、PC为长、宽、高建立长方体,该长方体的外接球就是三棱锥P-ABC的外接球.由球内接长方体的性质与长方体的对角线公式,算出PA2+PB2+PC2=16.
最后利用三角形面积公式与基本不等式加以计算,可得当PA=PB=PC时,S△PAB+S△PAC+S△PBC有最大值为8.
解答:解:∵
•
=0,
•
=0,
•
=0,
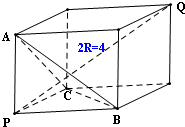
∴PA、PB、PC两两互相垂直,
如图所示,以PA、PB、PC为长、宽、高建立长方体,可得长方体的外接球就是三棱锥P-ABC的外接球,球的半径R=2.
∴PA
2+PB
2+PC
2=(2R)
2=16.
∵S
△PAB=
PA•PB≤
(PA
2+PB
2),S
△PAC=
PA•PC≤
(PA
2+PC
2),
S
△PBC=
PB•PC≤
(PB
2+PC
2),
∴S
△PAB+S
△PAC+S
△PBC≤
[(PA
2+PB
2)+(PA
2+PC
2)+(PB
2+PC
2)]=
(PA
2+PB
2+PC
2)=8.
当且仅当PA=PB=PC时,S
△PAB+S
△PAC+S
△PBC有最大值等于8.
故答案为:8
点评:本题给出三条侧棱两两垂直的三棱锥,已知它的外接球半径为2的情况下求侧面积的最大值.着重考查了向量的数量积及其运算性质、长方体的性质与对角线公式、球内接多面体与基本不等式等知识,属于中档题.




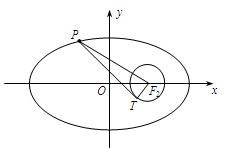 已知椭圆
已知椭圆