
已知数列 的前n项和为
的前n项和为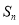 ,且满足
,且满足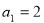 ,
,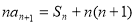 .
.
(1)求数列 的通项公式
的通项公式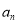 ;
;
(2)设 为数列{
为数列{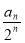 }的前n项和,求
}的前n项和,求 ;
;
(3)设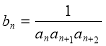 ,证明:
,证明: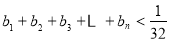 .
.
(1)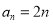 (2)
(2)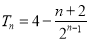 (3)见解析
(3)见解析
【解析】
试题分析:
(1)当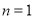 带入式子
带入式子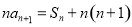 结合
结合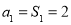 即可得到
即可得到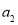 的值,当
的值,当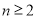 时,利用
时,利用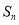 与
与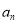 的关系(
的关系( )即可得到
)即可得到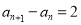 是一个常数,即可得到数列
是一个常数,即可得到数列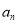 为等差数列,但是需要验证
为等差数列,但是需要验证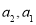 是否符合,进而证明
是否符合,进而证明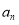 为等差数列,即可求的通项公式.
为等差数列,即可求的通项公式.
(2)把(1)中得到的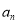 的通项公式带入
的通项公式带入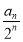 可得
可得 ,即为等差数列与等比数列的乘积,故需要利用错位相减法来求
,即为等差数列与等比数列的乘积,故需要利用错位相减法来求 的前n项和
的前n项和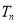 .
.
(3)把(1)得到的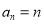 带入
带入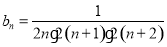 ,观察
,观察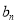 的通项公式为分式,为求其前n项和可以考虑利用裂项求和法.进行裂项
的通项公式为分式,为求其前n项和可以考虑利用裂项求和法.进行裂项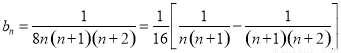 ,在进行求和就可以得到
,在进行求和就可以得到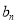 的前n项和为
的前n项和为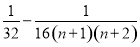 ,利用
,利用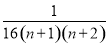 非负即可证明原不等式.
非负即可证明原不等式.
试题解析:
(1)由题意,当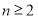 时,有
时,有 , (1分)
, (1分)
两式相减得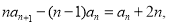 即
即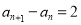 . (2分)
. (2分)
由 ,得
,得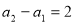 .
.
所以对一切正整数n,有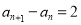 , (3分)
, (3分)
故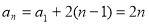 ,即
,即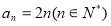 . (4分)
. (4分)
(2)由(1),得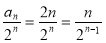 ,
,
所以 ① (5分)
① (5分)
①两边同乘以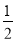 ,得
,得 ② (6分)
② (6分)
①-②,得 , (7分)
, (7分)
所以 , (8分)
, (8分)
故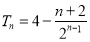 . (9分)
. (9分)
(3)由(1),得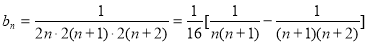 (12分)
(12分)
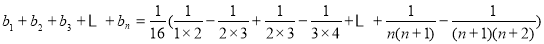
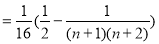 (13分)
(13分)
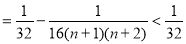 . (14分)
. (14分)
考点:裂项求和 错位相减 不等式


科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
已知非空有限实数集S的所有非空子集依次记为S1,S2,S3, ,集合Sk中所有元素的平均
值记为bk.将所有bk组成数组T:b1,b2,b3, ,数组T中所有数的平均值记为m(T).
(1)若S={1,2},求m(T);
(2)若S={a1,a2, ,an}(n∈N*,n≥2),求m(T).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)理科数学试卷(解析版) 题型:选择题
给出下列四个命题,其中假命题是( )
A.从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样;
B.样本方差反映了样本数据与样本平均值的偏离程度;
C.在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
D.设随机变量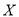 服从正态分布
服从正态分布 ,若
,若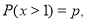 则
则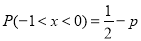 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)文科数学试卷(解析版) 题型:选择题
在某次测量中得到的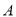 样本数据如下:82、84、84、86、86、86、88、88、88、88.若
样本数据如下:82、84、84、86、86、86、88、88、88、88.若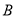 样本数据恰好是
样本数据恰好是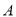 样本数据每一个数都加2后所得数据,则
样本数据每一个数都加2后所得数据,则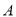 、
、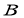 两个样本的下列数字特征对应相同的是( )
两个样本的下列数字特征对应相同的是( )
A.众数 B.平均数 C.中位数 D.方差
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟理科数学试卷(解析版) 题型:填空题
已知曲线C的极坐标方程为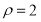 (
(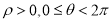 ),曲线C在点(2,
),曲线C在点(2,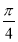 )处的切线为l,以极点为坐标原点,以极轴为x轴的正半轴建立直角坐标系,则l的直角坐标方程为 .
)处的切线为l,以极点为坐标原点,以极轴为x轴的正半轴建立直角坐标系,则l的直角坐标方程为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟理科数学试卷(解析版) 题型:选择题
下列命题中,真命题是 ( )
A. ,
,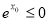 ;
;
B.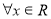 ,
,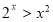 ;
;
C.“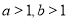 ”是“
”是“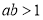 ”的充分不必要条件;
”的充分不必要条件;
D.设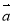 ,
,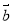 为向量,则“
为向量,则“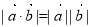 ”是“
”是“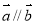 ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省湛江市高三高考模拟测试二文科数学试卷(解析版) 题型:填空题
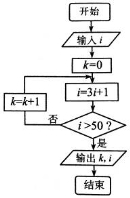
阅读如图所示的程序框图,若输入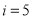 ,则输出的
,则输出的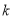 值为______________.
值为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com