
(A)30° (B)60° (C)90° (D)120°
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:

 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知矩形ACC1A1中,AA1=2,AC=4,B是AC上动点,过B作BB1∥A
已知矩形ACC1A1中,AA1=2,AC=4,B是AC上动点,过B作BB1∥A| A | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 2 |

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研数学试卷(理科)(解析版) 题型:解答题
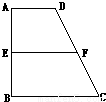
 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).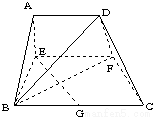
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试4 题型:选择题
(理)已知二面角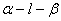 的平面角为
的平面角为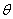 ,PA
,PA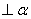 ,PB
,PB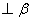 ,A,B为垂足,且PA=4,PB=5,设A、B到二面角的棱
,A,B为垂足,且PA=4,PB=5,设A、B到二面角的棱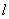 的距离为别为
的距离为别为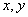 ,当
,当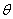 变化时,点
变化时,点 的轨迹是下列图形中的 ( )
的轨迹是下列图形中的 ( )
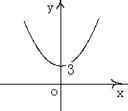
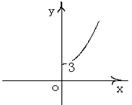
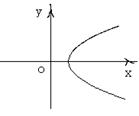
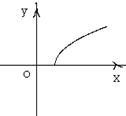
A B C D
(文)函数 上取得最大值时,x的值为 ( )
上取得最大值时,x的值为 ( )
A.0 B.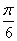 C.
C.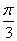 D.
D.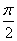
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com