
 =(sinB-sinA,sinB-sinC),
=(sinB-sinA,sinB-sinC), =(sinB+sinA,-sinC),并且
=(sinB+sinA,-sinC),并且 •
• =0.
=0.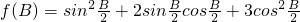 ,求f(B)的递增区间.
,求f(B)的递增区间. •
• =0
=0
 (6分)
(6分) =cosB+sinB+2=
=cosB+sinB+2= ,(8分)
,(8分)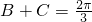 ,且B,C均为△ABC的内角,
,且B,C均为△ABC的内角,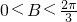 ,
, ,
, ,
,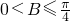 时,f(B)为递增函数,
时,f(B)为递增函数, (12分)
(12分) •
• =0,推出sin2B-sin2A-sinBsinC+sin2C=0,由正弦定理得b2-a2+bc+c2=0,然后利用余弦定理求出角A的大小.
=0,推出sin2B-sin2A-sinBsinC+sin2C=0,由正弦定理得b2-a2+bc+c2=0,然后利用余弦定理求出角A的大小.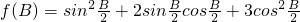 为
为 ,根据B+C的范围得到
,根据B+C的范围得到 ,求出函数f(B)的递增区间.
,求出函数f(B)的递增区间.

 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源:2010年高考试题(湖北卷)解析版(理) 题型:选择题
记实数 中的最大数为
中的最大数为 ,最小数为
,最小数为 已知
已知 的三边边长为a,b,c(
的三边边长为a,b,c( ),定义它的倾斜度为
),定义它的倾斜度为

则 是“
是“ 为等边三角”的
为等边三角”的
A.必要而不充分的条件 B.充分而不必要的条件
C.充要条件 D.既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| AB |
| AB |
| AC |
| AB |
| CB |
| BC |
| CA |
| A.等腰三角形 |
| B.直角三角开 |
| C.等腰直角三角形 |
| D.既非等腰三角形又非直角三角形 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年上海外国语大学附中高三(上)第一次周练数学试卷(解析版) 题型:选择题
 ,则△ABC为( )
,则△ABC为( )查看答案和解析>>
科目:高中数学 来源:2005-2006学年湖北省武汉市华中师大一附中高三(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,则△ABC为( )
,则△ABC为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com