
对于以下4个说法:①若函数 在
在 上单调递减,则实数
上单调递减,则实数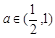 ;②若函数
;②若函数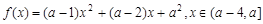 是偶函数,则实数
是偶函数,则实数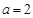 ;③若函数
;③若函数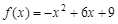 在区间
在区间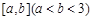 上有最大值9,最小值
上有最大值9,最小值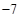 ,则
,则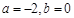 ;④
;④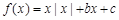 的图象关于点
的图象关于点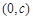 对称。其中正确的序号有 。
对称。其中正确的序号有 。
③④
解析试题分析:①若函数 在
在 上单调递减,则
上单调递减,则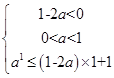 ,所以实数
,所以实数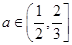 ,所以①错误;②若函数
,所以①错误;②若函数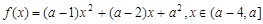 是偶函数,则实数
是偶函数,则实数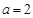 ,此命题错误,因为偶函数的定义域必须关于原点对称,所以
,此命题错误,因为偶函数的定义域必须关于原点对称,所以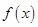 是非奇非偶函数;③因为
是非奇非偶函数;③因为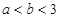 ,所以函数
,所以函数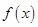 在区间
在区间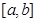 上单调递增,所以
上单调递增,所以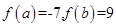 ,解得
,解得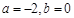 。所以函数
。所以函数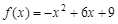 在区间
在区间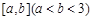 上有最大值9,最小值
上有最大值9,最小值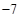 ,则
,则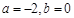 ;④因为
;④因为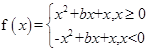 ,所以
,所以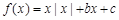 的图象关于点
的图象关于点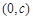 对称。
对称。
考点:指数函数的单调性;函数的奇偶性;二次函数在某闭区间上的最值;函数的对称性。
点评:此题较为综合,考到的知识点较多。这就要求我们平常对每个知识点都要掌握熟练,属于中档题。
判断函数的奇偶性有两步:一求函数的定义域,看定义域是否关于原点对称;二判断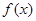 与
与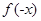 的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。
的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com