
已知半椭圆 与半椭圆
与半椭圆 组成的曲线称为“果圆”,其中
组成的曲线称为“果圆”,其中 。如图,设点
。如图,设点 ,
, ,
, 是相应椭圆的焦点,
是相应椭圆的焦点, ,
, 和
和 ,
, 是“果圆”
与
是“果圆”
与 ,
, 轴的交点,
轴的交点,
(1)若三角形 是边长为1的等边三角形,求“果圆”的方程;
是边长为1的等边三角形,求“果圆”的方程;
(2)若 ,求
,求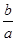 的取值范围;
的取值范围;
(3)一条直线与果圆交于两点,两点的连线段称为果圆的弦。是否存在实数 ,使得斜率为
,使得斜率为 的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有
的直线交果圆于两点,得到的弦的中点的轨迹方程落在某个椭圆上?若存在,求出所有 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(1)“果圆”方程为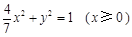 ,
,
(2)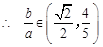
(3)在直线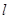 右侧,以
右侧,以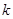 为斜率的平行弦的中点轨迹在直线
为斜率的平行弦的中点轨迹在直线 上,
上,
即不在某一椭圆上.
当 时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
 【解析】(1)
【解析】(1)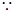
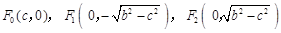 ,
,
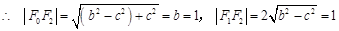 ,
,
于是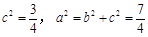 ,所求“果圆”方程为
,所求“果圆”方程为
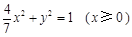 ,
,
(2)由题意,得 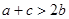 ,即
,即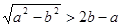 .
.
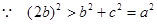 ,
,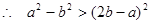 ,得
,得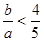 .
.
又 .
. 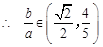 .
.
(3)设“果圆”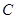 的方程为
的方程为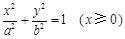 ,
,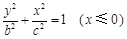 .
.
记平行弦的斜率为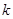 .
.
当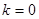 时,直线
时,直线 与半椭圆
与半椭圆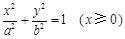 的交点是
的交点是
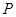
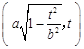 ,与半椭圆
,与半椭圆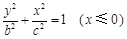 的交点是
的交点是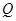
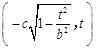 .
.
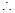
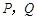 的中点
的中点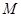
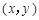 满足
满足
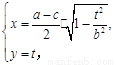 得
得 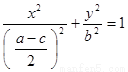 .
.
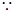
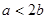 ,
,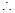
 .
.
综上所述,当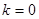 时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
时,“果圆”平行弦的中点轨迹总是落在某个椭圆上.
当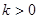 时,以
时,以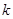 为斜率过
为斜率过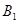 的直线
的直线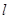 与半椭圆
与半椭圆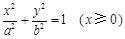 的交点是
的交点是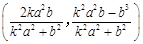 .
.
由此,在直线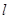 右侧,以
右侧,以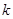 为斜率的平行弦的中点轨迹在直线
为斜率的平行弦的中点轨迹在直线 上,
上,
即不在某一椭圆上.
当 时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.
时,可类似讨论得到平行弦中点轨迹不都在某一椭圆上.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
已知:数列![]() 是由正数组成的等差数列,
是由正数组成的等差数列,![]() 是其前
是其前![]() 项的和,并且
项的和,并且![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求不等式![]() 对一切
对一切![]() 均成立最大实数
均成立最大实数![]() ;
;
(Ⅲ)对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高考预测数学试卷:填空解答题(解析版) 题型:选择题
甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一正四面体,碳原子位于该正四面体的中心,四个氢原子分别位于该正四面体的四个顶点上.若将碳原子和氢原子均视为一个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为 ,则以四个氢原子为顶点的这个正四面体的体积为( )
,则以四个氢原子为顶点的这个正四面体的体积为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三高考预测数学试卷(有解析) 题型:选择题
甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一正四面体,碳原子位于该正四面体的中心,四个氢原子分别位于该正四面体的四个顶点上.若将碳原子和氢原子均视为一个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为 ,则以四个氢原子为顶点的这个正四面体的体积为( )
,则以四个氢原子为顶点的这个正四面体的体积为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知:数列![]() 是由正数组成的等差数列,
是由正数组成的等差数列,![]() 是其前
是其前![]() 项的和,并且
项的和,并且![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求不等式![]() 对一切
对一切![]() 均成立最大实数
均成立最大实数![]() ;
;
(Ⅲ)对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
已知:数列![]() 是由正数组成的等差数列,
是由正数组成的等差数列,![]() 是其前
是其前![]() 项的和,并且
项的和,并且![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)求不等式![]() 对一切
对一切![]() 均成立最大实数
均成立最大实数![]() ;
;
(Ⅲ)对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com