
【题目】
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
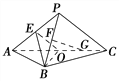
(Ⅰ)设G是OC的中点,证明:FG∥平面BOE;
(Ⅱ)证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
【答案】(Ⅰ)见解析;(Ⅱ) ![]()
【解析】试题分析:
(1)建立空间直角坐标系,利用题意结合平面的法向量和直线的方向向量可得FG∥平面BOE;
(2)设出点的坐标,利用空间直角坐标系可得点M到OA,OB的距离为![]() .
.
试题解析:
(Ⅰ)如图,连接OP,易知OB,OC,OP两两垂直,以点O为坐标原点,分别以OB,OC,OP所在直线为x轴,y轴,x轴,建立空间直角坐标系O-xyz,
则O(0,0,0),A(0,-8,0),B(8,0,0),C(0,8,0),P(0,0,6),E(0,-4,3),F(4,0,3).

由题意,得G(0,4,0)
因为![]() =(8,0,0),
=(8,0,0),![]() =(0,-4,3),
=(0,-4,3),
所以平面BOE的一个法向量为n=(0,3,4).
由![]() =(-4,4,-3),得n·
=(-4,4,-3),得n·![]() =0,即n⊥
=0,即n⊥![]() .
.
又直线FG不在平面BOE内,所以FG∥平面BOE.
(Ⅱ)设点M的坐标为(x0,y0,0),
则![]() =(x0-4,y0,-3).
=(x0-4,y0,-3).
所FM⊥平面BOE,所以![]() ∥n.
∥n.
因此x0=4,y0=-![]() ,即点M的坐标是(4,-
,即点M的坐标是(4,-![]() ,0).
,0).
在平面直角坐标系xOy中,△AOB的内部区域可表示为不等式组 
经检验,点M的坐标满足上述不等式组,所以在△AOB内存在一点M, 使FM⊥平面BOE.由点M的坐标得点M到OA,OB的距离分别为4,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,
, ![]() 为椭圆的半焦距,且
为椭圆的半焦距,且![]() ,过点
,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别交于另两点
分别交于另两点![]() ,
, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(3)若线段![]() 的中点在
的中点在![]() 轴上,求直线
轴上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∨q为真,求实数x的取值范围;
(2)若p是q的必要不充分要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以O为极点,
为参数),以O为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆![]() 的普通方程;
的普通方程;
(Ⅱ)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆C的交点为
与圆C的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a1+a3=10,S4=24.
(1)求数列{an}的通项公式;
(2)令Tn= ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com