
【题目】某学校因为寒假延期开学,根据教育部停课不停学的指示,该学校组织学生线上教学,高一年级在线上教学一个月后,为了了解线上教学的效果,在线上组织了数学学科考试,随机抽取50名学生的成绩并制成频率分布直方图如图所示.

(1)求m的值,并估计高一年级所有学生数学成绩在![]() 分的学生所占的百分比;
分的学生所占的百分比;
(2)分别估计这50名学生数学成绩的平均数和中位数.(同一组中的数据以该组区间的中点值作代表,结果精确到0.1)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 的一条直角是椭圆
的一条直角是椭圆![]() 的长轴,动直线
的长轴,动直线![]() ,当
,当![]() 过椭圆
过椭圆![]() 上一点
上一点![]() 且与圆
且与圆![]() 相交于点
相交于点![]() 时,弦
时,弦![]() 的最小值为
的最小值为![]() .
.
(1)求圆即椭圆![]() 的方程;
的方程;
(2)若直线![]() 是椭圆
是椭圆![]() 的一条切线,
的一条切线,![]() 是切线上两个点,其横坐标分别为
是切线上两个点,其横坐标分别为![]() ,那么以
,那么以![]() 为直径的圆是否经过
为直径的圆是否经过![]() 轴上的定点?如果存在,求出定点坐标;若不存在,请说明理由.
轴上的定点?如果存在,求出定点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.
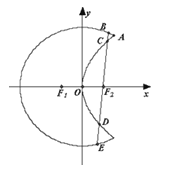
(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A. 甲地:总体均值为3,中位数为4 B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3 D. 丁地:总体均值为2,总体方差为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园里有一湖泊,其边界由两条线段![]() 和以
和以![]() 为直径的半圆弧
为直径的半圆弧![]() 组成,其中
组成,其中![]() 为2百米,
为2百米,![]() 为
为![]() .若在半圆弧
.若在半圆弧![]() ,线段
,线段![]() ,线段
,线段![]() 上各建一个观赏亭
上各建一个观赏亭![]() ,再修两条栈道
,再修两条栈道![]() ,使
,使![]() . 记
. 记![]() .
.
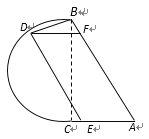
(1)试用![]() 表示
表示![]() 的长;
的长;
(2)试确定点![]() 的位置,使两条栈道长度之和最大.
的位置,使两条栈道长度之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》第三章“衰分”介绍了比例分配问题,“衰分”是按比例递减分配的意思,通常称递减的比例为“衰分比”.如:已知![]() 三人分配奖金的衰分比为
三人分配奖金的衰分比为![]() ,若
,若![]() 分得奖金1000元,则
分得奖金1000元,则![]() 所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
所分得奖金分别为900元和810元.某科研所四位技术人员甲、乙、丙、丁攻关成功,共获得奖金59040元,若甲、乙、丙、丁按照一定的“衰分比”分配奖金,且甲与丙共获得奖金32800元,则“衰分比”与丙所获得的奖金分别为( )
A.![]() ,12800元B.
,12800元B.![]() ,12800元
,12800元
C.![]() ,10240元D.
,10240元D.![]() ,10240元
,10240元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com