
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数且
为参数且![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
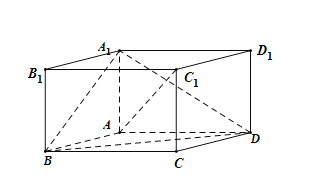
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() (α为参数)经过伸缩变换
(α为参数)经过伸缩变换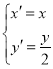 得到曲线C2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
得到曲线C2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求C2的普通方程;
(2)设曲线C3的极坐标方程为![]() ,且曲线C3与曲线C2相交于M,N两点,点P(1,0),求
,且曲线C3与曲线C2相交于M,N两点,点P(1,0),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为了帮助当地农民脱贫致富,开发了一种新型水果类食品,该食品生产成本为每件8元.当天生产当天销售时,销售价为每件12元,当天未卖出的则只能卖给水果罐头厂,每件只能卖5元.每天的销售量与当天的气温有关,根据市场调查,若气温不低于![]() ,则销售5000件;若气温位于
,则销售5000件;若气温位于![]() ,则销售3500件;若气温低于
,则销售3500件;若气温低于![]() ,则销售2000件.为制定今年8月份的生产计划,统计了前三年8月份的气温范围数据,得到下面的频数分布表:
,则销售2000件.为制定今年8月份的生产计划,统计了前三年8月份的气温范围数据,得到下面的频数分布表:
气温范围 (单位: |
|
|
|
|
|
天数 | 4 | 14 | 36 | 21 | 15 |
以气温范围位于各区间的频率代替气温范围位于该区间的概率.
(1)求今年8月份这种食品一天销售量(单位:件)的分布列和数学期望值;
(2)设8月份一天销售这种食品的利润为![]() (单位:元),当8月份这种食品一天生产量
(单位:元),当8月份这种食品一天生产量![]() (单位:件)为多少时,
(单位:件)为多少时,![]() 的数学期望值最大,最大值为多少
的数学期望值最大,最大值为多少![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 外的点
外的点![]() 在
在![]() 轴的右侧运动,且
轴的右侧运动,且![]() 到圆
到圆![]() 上的点的最小距离等于它到
上的点的最小距离等于它到![]() 轴的距离,记
轴的距离,记![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,以
两点,以![]() 为直径的圆
为直径的圆![]() 与平行于
与平行于![]() 轴的直线相切于点
轴的直线相切于点![]() ,线段
,线段![]() 交
交![]() 于点
于点![]() ,证明:
,证明:![]() 的面积是
的面积是![]() 的面积的四倍.
的面积的四倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
甲公司某员工A | 乙公司某员工B | |||||||||||||
3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
0 | 1 | 4 | 4 | 2 | 2 | 2 | ||||||||
每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是
A. 若命题p为真命题,命题q为假命题,则命题“pV(q)”为真命题
B. 命题“若a+b≠7,则a≠2或b≠5”为真命题
C. 命题“若x2-x=0,则x=0或x=1”的否命题为“若x2-x=0,则x≠0且x≠1”
D. 命题p: ![]() x>0,sinx>2x-1,则
x>0,sinx>2x-1,则![]() p为
p为![]() x>0,sinx≤2x-1
x>0,sinx≤2x-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com