
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 为左焦点,
为左焦点,![]() 为上顶点,
为上顶点,![]() 为右顶点,若
为右顶点,若![]() ,抛物线
,抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)是否存在过![]() 点的直线,与
点的直线,与![]() 和
和![]() 交点分别是
交点分别是![]() 和
和![]() ,使得
,使得![]() ?如果存在,求出直线的方程;如果不存在,请说明理由.
?如果存在,求出直线的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,从流水线上随机抽取100件产品,统计其质量指标值并绘制频率分布直方图(如图):
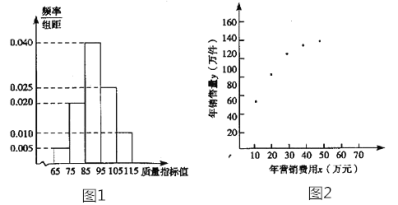
规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该企业为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年年营销费用
(单位:万件)的影响,对近5年年营销费用![]() 和年销售量
和年销售量![]() 数据做了初步处理,得到如图的散点图及一些统计量的值.
数据做了初步处理,得到如图的散点图及一些统计量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
⑦用所求的回归方程估计该企业应投人多少年营销费,才能使得该企业的年收益的预报值达到最大?(收益=销售利润营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() 其回归直线
其回归直线![]() 均斜率和截距的最小二乘估计分别为
均斜率和截距的最小二乘估计分别为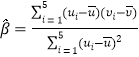 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球运动员的投篮命中率为![]() ,他想提高自己的投篮水平,制定了一个夏季训练计划
,他想提高自己的投篮水平,制定了一个夏季训练计划![]() 为了了解训练效果,执行训练前,他统计了10场比赛的得分,计算出得分的中位数为15分,平均得分为15分,得分的方差为
为了了解训练效果,执行训练前,他统计了10场比赛的得分,计算出得分的中位数为15分,平均得分为15分,得分的方差为![]() 执行训练后也统计了10场比赛的得分,成绩茎叶图如图所示:
执行训练后也统计了10场比赛的得分,成绩茎叶图如图所示:

![]() 请计算该篮球运动员执行训练后统计的10场比赛得分的中位数、平均得分与方差;
请计算该篮球运动员执行训练后统计的10场比赛得分的中位数、平均得分与方差;
![]() 如果仅从执行训练前后统计的各10场比赛得分数据分析,你认为训练计划对该运动员的投篮水平的提高是否有帮助?为什么?
如果仅从执行训练前后统计的各10场比赛得分数据分析,你认为训练计划对该运动员的投篮水平的提高是否有帮助?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着中国教育改革的不断深入,越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江,可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关,记者在北京,上海,深圳随机调查了100位市民,其中男性55位,女性45位.男性中有45位关注教育问题,其余的不关注教育问题;女性中有30位关注教育问题,其余的不关注教育问题.
(1)根据以上数据完成下列2×2列联表;
关注教育问题 | 不关注教育问题 | 合计 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合计 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
(2)能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系?
参考公式: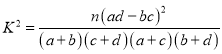 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
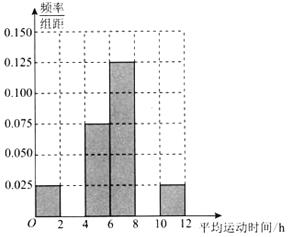
【题目】已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:h),汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:
平均运动时间 | 频数 | 频率 |
[0,2) | 15 | 0.05 |
[2,4) | m | 0.2 |
[4,6) | 45 | 0.15 |
[6,8) | 755 | 0.25 |
[8,10) | 90 | 0.3 |
[10,12) | p | n |
合计 | 300 | 1 |
(1)求抽取的女职工的人数;
(2)①根据频率分布表,求出m、n、p的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h的概率;
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中,有60名女职工每周的平均运动时间不低于4h,请完成以下2×2列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”.
附:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com