
 ,由此能够证明对于任意正整数k,数列Sk,S2k-Sk,S3k-S2k,…成等差数列.
,由此能够证明对于任意正整数k,数列Sk,S2k-Sk,S3k-S2k,…成等差数列.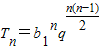 ,由T10=10,T20=20,得b110q45=10,b120q190=20,得
,由T10=10,T20=20,得b110q45=10,b120q190=20,得 ,
,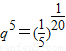 ,由此能够证明数列Tk,
,由此能够证明数列Tk,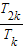 ,
, ,…成等比数列.
,…成等比数列.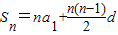 ,
, .
.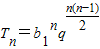 ,
,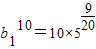 ,
,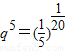 ,
, .…(12分)
.…(12分)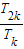 ,
, ,…成等比数列.…(14分)
,…成等比数列.…(14分)

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源:2015届四川省广元市高一下学期期中考试数学试卷(解析版) 题型:解答题
设Sn为等差数列{a n}的前n项和,已知a 9 =-2,S 8 =2.
(1)求首项a1和公差d的值;
(2)当n为何值时,Sn最大?并求出Sn的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com