
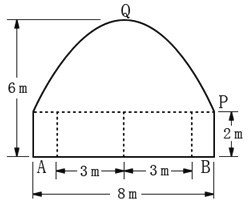
【题目】如图,一隧道内设双行线路,其截面由一长方形和一抛物线构成。为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部(抛物线)在竖直方向上的高度之差至少为0.5m,若行车道总宽度AB为6m,请计算通过隧道的车辆的限制高度(精确度为0.1m)
【答案】车辆通过隧道的限制高度是3.2米.
【解析】
根据题意可以建立适当的平面直角坐标系,从而可以得到抛物线的解析式,然后根据要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,可以得到当x=-3时,求出相应的y值,此时汽车的顶部离隧道的顶部距离至少是0.5m,从而可以求得车辆经过隧道时的限制高度是多少米.
取抛物线的顶点为原点,对称轴为y轴,建立直角坐标系,c(4,-4),
设抛物线方程x2=-2py(p>0),将点C代入抛物线方程得p=2,
∴抛物线方程为x2=-4y,行车道总宽度AB=6m,
∴将x=3代入抛物线方程,y=-2.25m,
∴限度为![]()
则车辆通过隧道的限制高度是3.2米.


科目:高中数学 来源: 题型:
【题目】某创业团队拟生产![]() 两种产品,根据市场预测,
两种产品,根据市场预测,![]() 产品的利润与投资额成正比(如图1),
产品的利润与投资额成正比(如图1),![]() 产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)
产品的利润与投资额的算术平方根成正比(如图2).(注: 利润与投资额的单位均为万元)

(注:利润与投资额的单位均为万元)
(1)分別将![]() 两种产品的利润
两种产品的利润![]() 、
、![]() 表示为投资额
表示为投资额![]() 的函数;
的函数;
(2)该团队已筹集到10 万元资金,并打算全部投入![]() 两种产品的生产,问:当
两种产品的生产,问:当![]() 产品的投资额为多少万元时,生产
产品的投资额为多少万元时,生产![]() 两种产品能获得最大利润,最大利润为多少?
两种产品能获得最大利润,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣![]() .
.
(1)若a>0,试判断f(x)在定义域内的单调性;
(2)若f(x)在[1,e]上的最小值为![]() ,求实数a的值;
,求实数a的值;
(3)若f(x)<x2在(1,+∞)上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C, AB=3,BC=5.
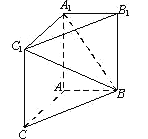
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com