
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(Ⅰ)(x﹣1)2+y2=25;(Ⅱ) ![]() ;(Ⅲ)x+2y﹣1=0.
;(Ⅲ)x+2y﹣1=0.
【解析】试题分析:(Ⅰ)圆心C是MN的垂直平分线与直线2x-y-2=0的交点,CM长为半径,进而可得圆的方程;
(Ⅱ)直线l过点(-2,5)且与圆C有两个不同的交点,则C到l的距离小于半径,进而得到k的取值范围;
(Ⅲ)求出AB的垂直平分线方程,将圆心坐标代入求出斜率,进而可得答案.
试题解析:
(I)MN的垂直平分线方程为:x﹣2y﹣1=0与2x﹣y﹣2=0联立解得圆心坐标为C(1,0)
R2=|CM|2=(﹣3﹣1)2+(3﹣0)2=25
∴圆C的标准方程为:(x﹣1)2+y2=25
(II)设直线![]() 的方程为:y﹣5=k(x+2)即kx﹣y+2k+5=0,设C到直线l的距离为d,
的方程为:y﹣5=k(x+2)即kx﹣y+2k+5=0,设C到直线l的距离为d,
则d=![]()
由题意:d<5 即:8k2﹣15k>0
∴k<0或k>![]()
又因为k>0
∴k的取值范围是(![]() ,+∞)
,+∞)
(III)设符合条件的直线![]() 存在,则AB的垂直平分线方程为:y+1=﹣
存在,则AB的垂直平分线方程为:y+1=﹣![]() (x﹣3)即:x+ky+k﹣3=0
(x﹣3)即:x+ky+k﹣3=0
∵弦的垂直平分线过圆心(1,0)∴k﹣2=0 即k=2
∵k=2>![]()
故符合条件的直线存在,l的方程:x+2y﹣1=0.


科目:高中数学 来源: 题型:
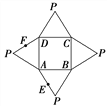
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系; ![]() 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.
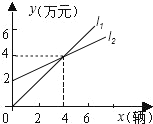
(1)写出销售收入与销售量之间的函数关系式;
(2)写出销售成本与销售量之间的函数关系式;
(3)当一天的销售量为多少辆时,销售收入等于销售成本;
(4)当一天的销售超过多少辆时,工厂才能获利?(利润=收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的上顶点到右顶点的距离为
)的上顶点到右顶点的距离为![]() ,左焦点为
,左焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程及
的标准方程及![]() 的取值范围;
的取值范围;
(Ⅱ)在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 恒为定值?若存在,求出点
恒为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
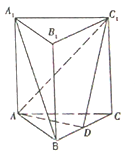
【题目】如图,三棱柱![]() 中,底面
中,底面![]() 为正三角形,
为正三角形, ![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得三棱锥
,使得三棱锥![]() 的体积是
的体积是![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C: ![]() ,点
,点![]() 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线![]() 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.

(1)若![]() ,且直线
,且直线![]() 的斜率为1,求以AB为直径的圆的方程;
的斜率为1,求以AB为直径的圆的方程;
(2)是否存在定点M,使得不论直线![]() 绕点M如何转动,
绕点M如何转动, ![]() 恒为定值?
恒为定值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),f(0)=-2,且对![]() ,y
,y![]() R,都有f(x+y)-f(y)=(x+2y+1)x.
R,都有f(x+y)-f(y)=(x+2y+1)x.
(1)求f(x)的表达式;
(2)已知关于x的不等式f(x)-ax+a+1![]() 的解集为A,若A[2,3],求实数a的取值范围;
的解集为A,若A[2,3],求实数a的取值范围;
(3)已知数列{![]() }中,
}中, ![]() ,
, ![]() ,记
,记![]() ,且数列{
,且数列{![]() 的前n项和为
的前n项和为![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。

区间 |
|
|
|
|
|
人数 |
| a | b |
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com