
【题目】Monte-Carlo方法在解决数学问题中有广泛的应用.下面利用Monte-Carlo方法来估算定积分![]() .考虑到
.考虑到![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,直线
轴,直线![]() 所围成的区域
所围成的区域![]() 的面积,如图,在
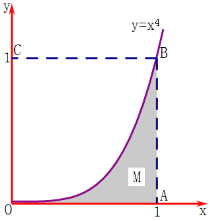
的面积,如图,在![]() 外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
(1)求X的期望![]() 和方差
和方差![]() ;
;
(2)求用以上方法估算定积分![]() 时,
时,![]() 的估计值与实际值之差在区间(-0.01,0.01)的概率.
的估计值与实际值之差在区间(-0.01,0.01)的概率.
附表:![]()
| 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |
科目:高中数学 来源: 题型:
【题目】下列命题正确的是
(1)命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l为直线,![]() ,
,![]() 为两个不同的平面,若
为两个不同的平面,若![]() ,
,![]() ,则
,则![]() ;
;
(3)给定命题p,q,若“![]() 为真命题”,则
为真命题”,则![]() 是假命题;
是假命题;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新鲜的荔枝很好吃,但摘下后容易变黑,影响卖相.某大型超市进行扶贫工作,按计划每年六月从精准扶贫户中订购荔枝,每天进货量相同且每公斤20元,售价为每公斤24元,未售完的荔枝降价处理,以每公斤16元的价格当天全部处理完.根据往年情况,每天需求量与当天平均气温有关.如果平均气温不低于25摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温低于15摄氏度,需求量为
公斤;如果平均气温低于15摄氏度,需求量为![]() 公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
平均气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(Ⅰ)假设该商场在这90天内每天进货100公斤,求这90天荔枝每天为该商场带来的平均利润(结果取整数);
(Ⅱ)若该商场每天进货量为200公斤,以这90天记录的各需求量的频率作为各需求量发生的概率,求当天该商场不亏损的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间y(分) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为![]() =
= ,
,![]() =
=![]() -
-![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国诗词大会”,某中学举行一次“诗词大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).

(1)求样本容量![]() 和频率分布直方图中
和频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,设随机变量![]() 表示所抽取的2名学生中得分在
表示所抽取的2名学生中得分在![]() 内的学生人数,求随机变量
内的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全国大学生机器人大赛是由共青团中央,全国学联,深圳市人民政府联合主办的赛事,是中国最具影响力的机器人项目,是全球独创的机器人竞技平台.全国大学生机器人大赛比拼的是参赛选手们的能力,坚持和态度,展现的是个人实力以及整个团队的力量.2015赛季共吸引全国240余支机器人战队踊跃报名,这些参赛战队来自全国六大赛区,150余所高等院校,其中不乏北京大学,清华大学,上海交大,中国科大,西安交大等众多国内顶尖高校,经过严格筛选,最终由111支机器人战队参与到2015年全国大学生机器人大赛的激烈角逐之中,某大学共有“机器人”兴趣团队1000个,大一、大二、大三、大四分别有100,200,300,400个,为挑选优秀团队,现用分层抽样的方法,从以上团队中抽取20个团队.
(1)应从大三抽取多少个团队?
(2)将20个团队分为甲、乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲、乙两组的分数如下:
甲:125,141,140,137,122,114,119,139,121,142
乙:127,116,144,127,144,116,140,140,116,140
从甲、乙两组中选一组强化训练,备战机器人大赛.
(i)从统计学数据看,若选择甲组,理由是什么?若选择乙组,理由是什么?
(ii)从乙组中不低于140分的团队中任取两个团队,求至少有一个团队为144分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.

(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com