
【题目】数据x1,x2,x3,x4,x5的方差是2,则数据x1-1,x2-1,x3-1,x4-1,x5-1的方差是____.
【答案】2
【解析】
根据平均数,方差的公式进行计算.
依题意,得![]() (x1+x2+x3+x4+x5),
(x1+x2+x3+x4+x5),
∴x1﹣1、x2﹣1、x3﹣1、x4﹣1、x5﹣1的平均数为
![]() [(x1﹣1)+(x2﹣1)+(x3﹣1)+(x4﹣1)+(x5﹣1)]
[(x1﹣1)+(x2﹣1)+(x3﹣1)+(x4﹣1)+(x5﹣1)]
=![]() (x1+x2+x3+x4+x5)﹣1=
(x1+x2+x3+x4+x5)﹣1=![]() 1,
1,
∵数据x1,x2,x3,x4,x5的方差
S2![]() [(x1
[(x1![]() )2+(x2
)2+(x2![]() )2+(x3
)2+(x3![]() )2+(x4
)2+(x4![]() )2+(x5
)2+(x5![]() )2]=2,
)2]=2,
∴数据x1﹣1、x2﹣1、x3﹣1、x4﹣1、x5﹣1的方差
S′2![]() [(x1﹣1﹣
[(x1﹣1﹣![]() 1)2+(x2﹣1﹣
1)2+(x2﹣1﹣![]() 1)2+(x3﹣1﹣
1)2+(x3﹣1﹣![]() 1)2+(x4﹣1﹣
1)2+(x4﹣1﹣![]() 1)2+(x5﹣1﹣
1)2+(x5﹣1﹣![]() 1)2]
1)2]
![]() [(x1
[(x1![]() )2+(x2
)2+(x2![]() )2+(x3
)2+(x3![]() )2+(x4
)2+(x4![]() )2+(x5
)2+(x5![]() )2]=2.
)2]=2.
故答案为2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,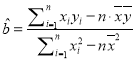 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,对于函数![]() ,称向量
,称向量![]() 为函数
为函数![]() 的伴随向量,同时称函数
的伴随向量,同时称函数![]() 为向量
为向量![]() 的伴随函数.
的伴随函数.
(1)设函数![]() ,试求
,试求![]() 的伴随向量
的伴随向量![]() ;
;
(2)记向量![]() 的伴随函数为
的伴随函数为![]() ,求当
,求当![]() 且
且![]() 时
时![]() 的值;
的值;
(3)由(1)中函数![]() 的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移
的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,已知
的图象,已知![]() ,
,![]() ,问在
,问在![]() 的图象上是否存在一点P,使得
的图象上是否存在一点P,使得![]() .若存在,求出P点坐标;若不存在,说明理由.
.若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() .
.
(1)若f(x)有两个极值点,求实数m的取值范围:
(2)若函数![]() 有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且
有且只有三个不同的零点,分别记为x1,x2,x3,设x1<x2<x3,且![]() 的最大值是e2,求x1x3的最大值.
的最大值是e2,求x1x3的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (
(![]() ,
,![]() ),
),![]() ,
,![]() 是双曲线的两个顶点,
是双曲线的两个顶点,![]() 是双曲线上的一点,且与点
是双曲线上的一点,且与点![]() 在双曲线的同一支上,
在双曲线的同一支上,![]() 关于
关于![]() 轴的对称点是
轴的对称点是![]() ,若直线
,若直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,且
,且![]() ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com