[题目]随着生活水平的提高.人们对空气质量的要求越来越高.某机构为了解公众对“车辆限行的态度.随机抽查人,并将调查情况进行整理后制成下表:年龄(岁)频数赞成人数(1)完成被调查人员年龄的频率分布直方图.并求被调査人员中持赞成态度人员的平均年龄约为多少岁?(2)若从年龄在的被调查人员中各随机选取人进行调查.请写出所有的基本亊题目和参考答案——青夏教育精英家教网—

【题目】随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查人,并将调查情况进行整理后制成下表：

年龄（岁）
频数
赞成人数

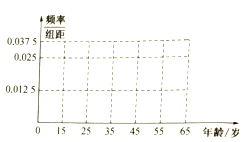
（1）完成被调查人员年龄的频率分布直方图，并求被调査人员中持赞成态度人员的平均年龄约为多少岁？

（2）若从年龄在的被调查人员中各随机选取人进行调查.请写出所有的基本亊件,并求选取人中恰有人持不赞成态度的概率.

【答案】（1）42.6岁；（2）.

【解析】试题分析：（1）依次求出个小组的频率/组距，进而完成直方图；

（2）用古典概型的原理列举出基本事件求概率即可.

试题解析：

(1)被调查人员年龄的频率分布直方图如图所示：

被调查人员持赞成态度人的平均年龄约为（岁）.

(2)设中赞成的人分别为，不赞成的人为，

中赞成的人分别为，不赞成的人为.基本事件为：

，

基本事件共有个，其中恰有人持不赞成态度的基本事件为个.据古典概型知：恰有人持不赞成态度的概率.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】函数f（x）=loga（x+1），（a＞0，a≠1）的图象经过点（﹣ ，﹣2），图象上有三个点A，B，C，它们的横坐标依次为t﹣1，t，t+1，（t≥1），记三角形ABC的面积为S（t），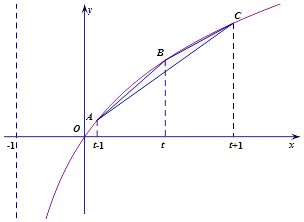

（1）求f（x）的表达式；
（2）求S（1）；
（3）是否存在正整数m，使得对于一切不小于1的t，都有S（t）＜m，若存在求的最小值，若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知P（﹣2，3）是函数y= 图象上的点，Q是双曲线在第四象限这一分支上的动点，过点Q作直线，使其与双曲线y= 只有一个公共点，且与x轴、y轴分别交于点C、D，另一条直线y= x+6与x轴、y轴分别交于点A、B．则
（1）O为坐标原点，三角形OCD的面积为．
（2）四边形ABCD面积的最小值为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．
（Ⅰ）证明：PA⊥BD；
（Ⅱ）设PD=AD=1，求直线PC与平面ABCD所成角的正切值．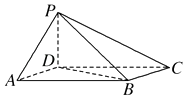

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知集合A={x|1＜x＜3}，集合B={x|2m＜x＜1﹣m}．
（1）若AB，求实数m的取值范围；
（2）若A∩B=，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司制定了一个激励销售人员的奖励方案：当销售利润不超过8万元时，按销售利润的15%进行奖励；当销售利润超过8万元时，若超出A万元，则超出部分按log5（2A+1）进行奖励．记奖金为y（单位：万元），销售利润为x（单位：万元）．
（1）写出奖金y关于销售利润x的关系式；
（2）如果业务员小江获得3.2万元的奖金，那么他的销售利润是多少万元？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知关于x的不等式：|2x﹣m|≤1的整数解有且仅有一个值为2．
（1）求整数m的值；
（2）在（1）的条件下，解不等式：|x﹣1|+|x﹣3|≥m．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设等差数列{an}的前n项和为Sn ，已知a3=24，a6=18．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列{an}的前n项和Sn；
（Ⅲ）当n为何值时，Sn最大，并求Sn的最大值．