
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() ,数列
,数列![]() 是正项等比数列,且
是正项等比数列,且![]() ,
,![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)记![]() ,是否存在正整数
,是否存在正整数![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() 成立?若存在,求出M的最小值;若不存在,请说明理由.
成立?若存在,求出M的最小值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体,直角三角形也可以推广到直角四面体,如果四面体![]() 中棱
中棱![]() 两两垂直,那么称四面体
两两垂直,那么称四面体![]() 为直角四面体. 请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论
为直角四面体. 请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论![]() 中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中
中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中![]() 表示斜边上的高,
表示斜边上的高,![]() 分别表示内切圆与外接圆的半径)
分别表示内切圆与外接圆的半径)
直角三角形 | 直角四面体 | |
条件 |
|
|
结论1 |
| |
结论2 |
| |
结论3 |
| |
结论4 |
| |
结论5 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知集合A={x|-2<x<0},B={x|y=![]() }
}
(1)求(RA)∩B;
(2)若集合C={x|a<x<2a+1}且CA,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
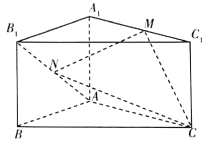
(1)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(2)若点![]() 为
为![]() 的中点且
的中点且![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 是偶函数,设
是偶函数,设![]()
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() ≥0在区间(1,e2]上恒成立,求实数
≥0在区间(1,e2]上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了全面贯彻党的教育方针,坚持以人文本、德育为先,全面推进素质教育,让学生接触自然,了解社会,拓宽视野,丰富知识,提高社会实践能力和综合素质,减轻学生过重负担,培养学生兴趣爱好,丰富学生的课余生活,使广大学生在社会实践中,提高创新精神和实践能力,树立学生社会责任感,因此学校鼓励学生利用课余时间参加社会活动实践。寒假归来,某校高三(2)班班主任收集了所有学生参加社会活动信息,整理出如图所示的图。
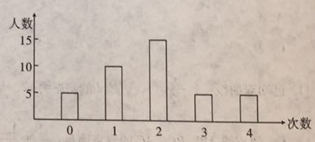
(1)求高三(2)班同学人均参加社会活动的次数;
(2)求班上的小明同学仅参加1次社会活动的概率;
(3)用分层抽样的方法从班上参加活动2次及以上
的同学中抽取一个容量为5的样本,从这5人中任选3人,其中仅有两人参加2次活动的概率。.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com