
【题目】近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月![]() ,
,![]() 两种移动支付方式的使用情况,从全校学生随机抽取了100人,发现使用
两种移动支付方式的使用情况,从全校学生随机抽取了100人,发现使用![]() 或
或![]() 支付方式的学生共有90人,使用
支付方式的学生共有90人,使用![]() 支付方式的学生共有70人,
支付方式的学生共有70人,![]() ,
,![]() 两种支付方式都使用的有60人,则该校使用
两种支付方式都使用的有60人,则该校使用![]() 支付方式的学生人数与该校学生总数比值的估计值为______.
支付方式的学生人数与该校学生总数比值的估计值为______.
科目:高中数学 来源: 题型:
【题目】设抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() ,以
,以![]() 为圆心的圆
为圆心的圆![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 的纵坐标为
的纵坐标为![]() ,
,![]() 是圆
是圆![]() 与
与![]() 轴的不同于
轴的不同于![]() 的一个交点.
的一个交点.
(1)求抛物线![]() 与圆
与圆![]() 的方程;
的方程;
(2)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为3的疋方形,侧面
是边长为3的疋方形,侧面![]() 与底面
与底面![]() 垂直,过点
垂直,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,且满足
,且满足![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]()
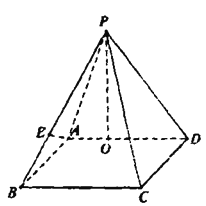
(1)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)当![]() 取何值时,二面角
取何值时,二面角![]() 的正弦值为
的正弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
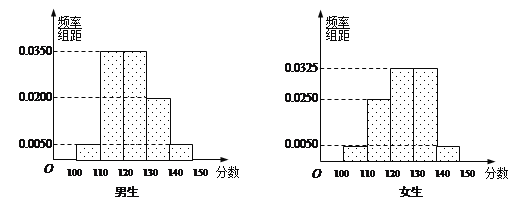
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
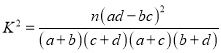 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上的两个点,点
上的两个点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .设抛物线
.设抛物线![]() 的焦点在直线
的焦点在直线![]() 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且![]() ,过
,过![]() 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为![]() . 判断四边形
. 判断四边形![]() 是否为梯形,并说明理由.
是否为梯形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
| 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0 16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0 40 |
第4组 | [80,90) | ▓ | 0 08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |
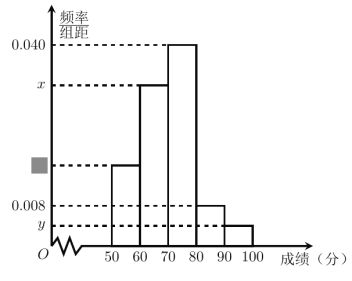
(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com