
【题目】已知椭圆![]() :
:![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() :
:![]() 的焦点重合,且椭圆的离心率为
的焦点重合,且椭圆的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点,![]() 为原点,求
为原点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)抛物线![]() :
:![]() 的焦点坐标为
的焦点坐标为![]() ,则
,则![]() ,再根据离心率求出a,即可求出b,可得椭圆
,再根据离心率求出a,即可求出b,可得椭圆![]() 的方程;
的方程;
(2)由题意知直线![]() 的斜率
的斜率![]() 存在,设其方程为
存在,设其方程为![]() ,设
,设![]() ,将直线与椭圆联立成方程组,利用根与系数关系求出
,将直线与椭圆联立成方程组,利用根与系数关系求出![]() 和
和![]() ,代入弦长公式即可求出
,代入弦长公式即可求出![]() ,再利用点到直线距离公式求原点到直线
,再利用点到直线距离公式求原点到直线![]() 的距离
的距离![]() ,从而可求
,从而可求![]() ,利用换元法根据基本不等式即可求出
,利用换元法根据基本不等式即可求出![]() 面积的最大值.
面积的最大值.
(1)抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,则
,则![]() ,
,
又椭圆的离心率![]() ,所以
,所以![]() ,
,
所以![]() ,
,
故所求椭圆的标准方程为![]() .
.
(2)由题意知直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
设![]() ,则
,则
由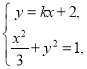 消去
消去![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,
,
由根与系数的关系可得![]() ,
,![]() ,
,
又原点到直线![]() 的距离
的距离![]() ,
,
![]()
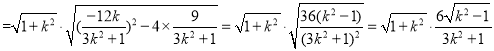
所以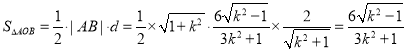 ,
,
令![]() ,则
,则![]() ,所以
,所以
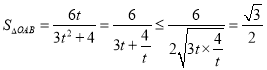 ,当且仅当
,当且仅当![]() ,即
,即![]() ,此时
,此时![]() ,
,
所以![]() 的面积的最大值为
的面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商家计划投入10万元经销甲,乙两种商品,根据市场调查统计,当投资额为![]() 万元,经销甲,乙两种商品所获得的收益分别为
万元,经销甲,乙两种商品所获得的收益分别为![]() 万元与
万元与![]() 万元,其中
万元,其中![]() ,
,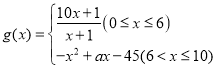 ,当该商家把10万元全部投入经销乙商品时,所获收益为5万元.
,当该商家把10万元全部投入经销乙商品时,所获收益为5万元.
(1)求实数a的值;
(2)若该商家把10万元投入经销甲,乙两种商品,请你帮他制订一个资金投入方案,使他能获得最大总收益,并求出最大总收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求实数m的值;
(2)若ARB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有______
①平均数不受少数几个极端值的影响,中位数受样本中的每一个数据影响;
②抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大
③用样本的频率分布估计总体分布的过程中,样本容量越大,估计越准确.
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:①“若x2+ y2 ≠0,则x,y不全为零”的否命题;②“正多边形都相似”的逆命题;③“若m>0,则x2+x-m=0有实根”的逆否命题;其中真命题的序号是____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com