
已知函数f(x)=2ax-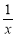 -(2+a)lnx(a≥0).
-(2+a)lnx(a≥0).
(1)当a=0时,求f(x)的极值;
(2)当a>0时,讨论f(x)的单调性;
(3)若对任意的a∈(2,3),x1,x2∈[1,3],恒有(m-ln3)a-2ln3>|f(x1)-f(x2)|成立,求实数m的取值范围。
(1)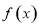 的极大值为
的极大值为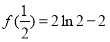 ,无极小值.(3)
,无极小值.(3) 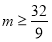
【解析】
试题分析:(1)求已知函数的极值,利用导数法,即求定义域,求导,求导数为0与单调区间,判断极值点求出极值. (2) 求定义域,求导.利用数形结合思想讨论导数(含参数二次不等式)的符号求f(x)的单调区间,讨论二次含参数不等式注意按照定性(二次项系数是否为0),开口,判别式,两根大小得顺序依次进行讨论,进而得到函数f(x)的单调性(注意单调区间为定义域的子集)(3)这是一个恒成立问题,只需要(m-ln3)a-2ln3>(|f(x1)-f(x2)|)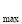 ,故求解确定|f(x1)-f(x2)|最大值很关键,分析可以发现(|f(x1)-f(x2)|)
,故求解确定|f(x1)-f(x2)|最大值很关键,分析可以发现(|f(x1)-f(x2)|)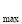 =
=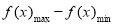 ,故可以利用第二问单调性来求得函数的最值进而得到(|f(x1)-f(x2)|)
,故可以利用第二问单调性来求得函数的最值进而得到(|f(x1)-f(x2)|)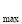 . (m-ln3)a-2ln3>(|f(x1)-f(x2)|)
. (m-ln3)a-2ln3>(|f(x1)-f(x2)|)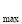 对于任意的a∈(2, 3)恒成立,则也是一个恒成立问题,可以采用分离参数法就可以求的m的取值范围.
对于任意的a∈(2, 3)恒成立,则也是一个恒成立问题,可以采用分离参数法就可以求的m的取值范围.
试题解析:(1)当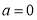 时,
时,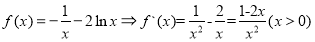 ,由
,由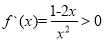 ,解得
,解得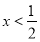 ,可知
,可知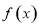 在
在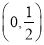 上是增函数,在
上是增函数,在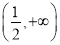 上是减函数.
上是减函数.
∴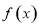 的极大值为
的极大值为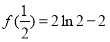 ,无极小值.
,无极小值.
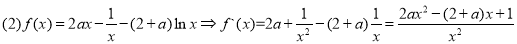
①当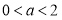 时,
时,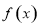 在
在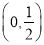 和
和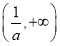 上是增函数,在
上是增函数,在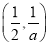 上是减函数;
上是减函数;
②当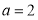 时,
时,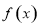 在
在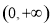 上是增函数;
上是增函数;
③当 时,
时,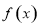 在
在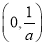 和
和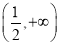 上是增函数,在
上是增函数,在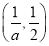 上是减函数 8分
上是减函数 8分
(3)当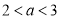 时,由(2)可知
时,由(2)可知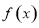 在
在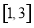 上是增函数,
上是增函数,
∴ .
.
由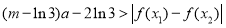 对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
对任意的a∈(2, 3),x1, x2∈[1, 3]恒成立,
∴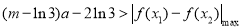
即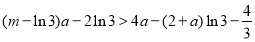 对任意
对任意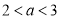 恒成立,
恒成立,
即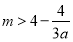 对任意
对任意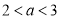 恒成立,由于当
恒成立,由于当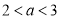 时,
时,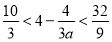 ,∴
,∴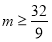 .
.
考点: 导数 恒成立问题 不等式


科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
过抛物线C: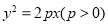 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求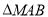 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试理科数学试卷(解析版) 题型:选择题
如图,正方体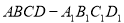 的棱长为
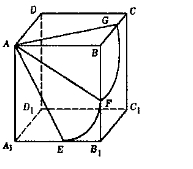
的棱长为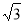 ,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
,以顶点A为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( )
A.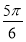 B.
B. C.
C.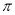 D.
D.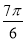
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:选择题
程序框图如图所示:
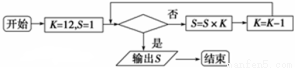
如果上述程序运行的结果S=1320,那么判断框中应填入( )
A.K<10! B.K≤10! C.K<9? ! D.K≤11!
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知函数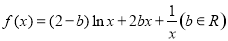 .
.
(1)当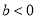 时,求
时,求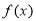 的单调区间;
的单调区间;
(2)当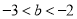 时,若存在
时,若存在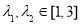 , 使得
, 使得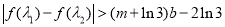 成立,求实数
成立,求实数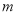 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com