
【题目】已知数列![]() 、
、![]() ,其中,
,其中, ![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() 有
有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若数列![]() 满足
满足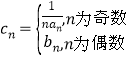 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1) ![]()
![]() .
.
(2) ![]() 的最小值为16.
的最小值为16.
(3) 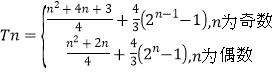 .
.
【解析】试题分析:第一问将式子变形,得到两项的比值,之后用累乘法求得通项公式,一定需要注意对![]() 进行验证;第二问转化成最值来处理,第三问需要对
进行验证;第二问转化成最值来处理,第三问需要对![]() 为奇数和
为奇数和![]() 为偶数两种情况进行讨论求得结果.
为偶数两种情况进行讨论求得结果.
(1)由![]() ,即
,即![]() ,
,![]() .
.
又![]() ,所以
,所以![]()
![]()
![]() . ……………………2分
. ……………………2分
当![]() 时,上式成立,故
时,上式成立,故![]()
![]() ……………………3分
……………………3分
因为![]() ,所以
,所以![]() 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,
故![]() . ……………………5分
. ……………………5分
(2) 由(1)知![]() ,则
,则
![]() .……………………7分
.……………………7分
假设存在自然数![]() ,使得对于任意
,使得对于任意![]() 有
有![]() 恒成立,即
恒成立,即![]() 恒成立,由
恒成立,由![]() ,解得
,解得![]() . ……………………9分
. ……………………9分
所以存在自然数![]() ,使得对于任意
,使得对于任意![]() 有
有![]() 恒成立,此时,
恒成立,此时, ![]() 的最小值为16. ……………………………………10分
的最小值为16. ……………………………………10分
(3)当![]() 为奇数时,
为奇数时,
![]()
![]()
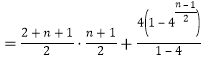
![]() ;………………13分
;………………13分
当![]() 为偶数时,
为偶数时,
![]()
![]()
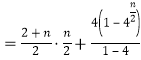
![]() . ………………15分
. ………………15分
因此
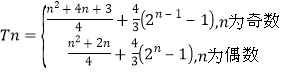 ………………16分
………………16分


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的首项a1=1,且(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;、
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 ![]() 和
和 ![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数ξ的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系 ![]() 中,直线
中,直线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)写出直线 ![]() 的普通方程及圆
的普通方程及圆 ![]() 的直角坐标方程;
的直角坐标方程;
(2)点 ![]() 是直线
是直线 ![]() 上的点,求点
上的点,求点 ![]() 的坐标,使
的坐标,使 ![]() 到圆心
到圆心 ![]() 的距离最小.
的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出呼叫信号,我海军舰艇在![]() 处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为
处获悉后,立即测出该渔船在方位角(从指北方向顺时针转到目标方向线的水平角)为![]() ,距离为15海里的
,距离为15海里的![]() 处,并测得渔船正沿方位角为
处,并测得渔船正沿方位角为![]() 的方向,以15海里/小时的速度向小岛
的方向,以15海里/小时的速度向小岛![]() 靠拢,我海军舰艇立即以
靠拢,我海军舰艇立即以![]() 海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
海里/小时的速度前去营救,求舰艇靠近渔船所需的最少时间和舰艇的航向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com