Question

【题目】已知函数f（x）=|xex+1|，关于x的方程f2（x）+2sinαf（x）+cosα=0有四个不等实根，sinα﹣cosα≥λ恒成立，则实数λ的最大值为（ ）
A.﹣
B.﹣
C.﹣
D.﹣1

Answer 1

【答案】A
【解析】解：f（x）=|xex+1|= 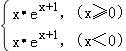，当x≥0时，f′（x）=ex+1+xex+1≥0恒成立，所以f（x）在[0，+∞）上为增函数；
当x＜0时，f′（x）=﹣ex+1﹣xex+1=﹣ex+1（x+1），
由f′（x）=0，得x=﹣1，当x∈（﹣∞，﹣1）时，f′（x）=﹣ex+1（x+1）＞0，f（x）为增函数，
当x∈（﹣1，0）时，f′（x）=﹣ex+1（x+1）＜0，f（x）为减函数，
所以函数f（x）=|xex+1|的极大值为f（﹣1）=|（﹣1）e0|=1，
极小值为：f（0）=0，
令f（x）=m，由韦达定理得：m1+m2=﹣2sinα，m1m2=cosα，
此时若sinα＞0，则当m1＜0，且m2＜0，
此时方程f2（x）+2sinαf（x）+cosα=0至多有两个实根，
若sinα＜0，则当m1＞0，且m2＞0，
要使方程f2（x）+2sinαf（x）+cosα=0有四个实数根，
则方程m2+2sinαm+cosα=0应有两个不等根，
且一个根在（0，1）内，一个根在（1，+∞）内，
再令g（m）=m2+2sinαm+cosα，
因为g（0）=cosα＞0，①
△=4sin2α﹣4cosα＞0，则1﹣cos2α﹣cosα＞0，②
则只需g（1）＜0，即1+2sinα+cosα＜0，
所以0＜cosα＜﹣1﹣2sinα，③
由①②解得：0＜cosα＜ ，④
由③④得到：sinα＜ ， ＜cosα＜ ，
所以sinα﹣cosα＜ ﹣ =﹣ ，
∴λ≤﹣ ．
故选：A．