
分析 利用条件x+2y+z=1,构造柯西不等式(x+y+z)2≤(x2+y2+z2)(12+22+12)进行解题即可.
解答 解:由柯西不等式,得(x+2y+z)2≤(12+22+12)•(x2+y2+z2),
即$x+2y+z≤\sqrt{{1^2}+{2^2}+{1^2}}•\sqrt{{x^2}+{y^2}+{z^2}}$,…(5分)
又因为x+2y+z=1,所以${x^2}+{y^2}+{z^2}≥\frac{1}{6}$,
当且仅当$\frac{x}{1}=\frac{y}{2}=\frac{z}{1}$,即$x=z=\frac{1}{6},y=\frac{1}{3}$时取等号.
综上,${({{x^2}+{y^2}+{z^2}})_{min}}=\frac{1}{6}$.…(10分)
点评 本题主要考查了函数的最值,以及柯西不等式的应用,解题的关键是利用(x+2y+z)2≤(x2+y2+z2)(12+22+12)进行解决.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
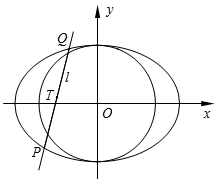 在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.
在平面直角坐标系xOy中,已知圆O:x2+y2=b2经过椭圆$E:\frac{x^2}{4}+\frac{y^2}{b^2}=1$(0<b<2)的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 斤 | B. | 9 斤 | C. | 9.5斤 | D. | 12 斤 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
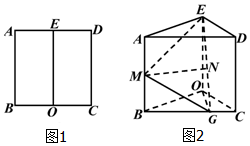 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com