
【题目】如图,已知四棱锥![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
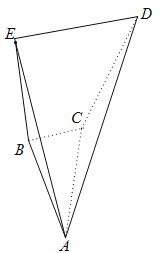
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:在线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,并指明点
,并指明点![]() 的位置;
的位置;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析(2)证明见解析;点![]() 是
是![]() 的中点(3)
的中点(3)![]()
【解析】
(1)根据所给线段,应用勾股定理逆定理可证明![]() ,结合
,结合![]() 平面
平面![]() 可知
可知![]() ,从而由线面垂直判定定理即可证明
,从而由线面垂直判定定理即可证明![]() 平面
平面![]() ;
;
(2)根据垂直关系,以点![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,写出各个点的坐标,设
轴建立空间直角坐标系,写出各个点的坐标,设![]() ,表示出
,表示出![]() 后结合平面向量数量积垂直的坐标关系,即可求得
后结合平面向量数量积垂直的坐标关系,即可求得![]() 的值,进而确定
的值,进而确定![]() 的位置.
的位置.
(3)根据空间直角坐标系,求得平面![]() 的法向量
的法向量![]() 平面
平面![]() 的法向量
的法向量![]() ,由空间向量数量积定义求得两个法向量夹角的余弦值,结合二面角为锐二面角,即可求得二面角
,由空间向量数量积定义求得两个法向量夹角的余弦值,结合二面角为锐二面角,即可求得二面角![]() 的大小.
的大小.
(1)证明:![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]() ,
,
![]() 平面
平面![]() .
.
(2)证明:以点![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]() ,
,
![]() ,解得
,解得![]() ,
,
所以点![]() 是
是![]() 的中点.
的中点.
(3)设平面![]() 的法向量为
的法向量为![]()
![]() ,
,![]() ,
,
所以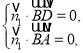 即
即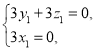
令![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() ,
,![]() ,
,
所以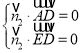 即
即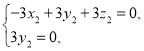 ,
,
令![]() ,则
,则![]() ,
,
所以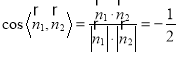 .
.
由图知二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的大小为
的大小为![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且a≠1,函数
且a≠1,函数![]() .
.
(1)判断并证明f(x)和g(x)的奇偶性;
(2)求g(x)的值域;
(3)若x∈R,都有|f(x)|≥|g(x)|成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究每周累计户外暴露时间是否足够(单位:小时)与近视发病率的关系,对某中学一年级![]() 名学生进行不记名问卷调查,得到如下数据:
名学生进行不记名问卷调查,得到如下数据:

(1)用样本估计总体思想估计该中学一年级学生的近视率;
(2)能否认为在犯错误的概率不超过![]() 的前提下认为不足够的户外暴露时间与近视有关系?
的前提下认为不足够的户外暴露时间与近视有关系?
附: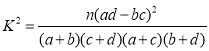 .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
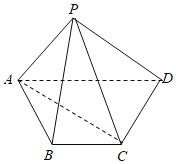
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为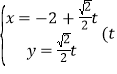 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com