Question

曲线y=x²+3在点（1，4）处的切线与两坐标轴的交点为A、B，向圆x²+y²+2x-8=0内随机投一点，则该点落在△AOB内的概率是    ．

Answer 1

【答案】分析：先求切线方程，求得A，B的坐标，确定△AOB在圆的内部，由此可求点落在△AOB内的概率．
解答：解：由y=x²+3，可得y′=2x，∴x=1时，y′=2
∴曲线y=x²+3在点（1，4）处的切线方程为y-4=2（x-1），即2x-y+2=0
令x=0，则y=2，令y=0，则x=-1，即A（-1，0），B（0，2），
∵x²+y²+2x-8=0，即（x+1）²+y²=9，∴圆心为（-1，0），半径为3
∴A，B均在圆内
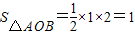
∵，S_圆=9π
∴该点落在△AOB内的概率是
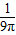
故答案为：
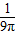点评：本题考查概率的计算，考查切线方程，考查学生的计算能力，确定切线方程是关键．