练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

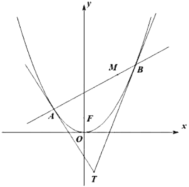
    【题目】已知抛物线上的点到其焦点距离为3，过抛物线外一动点作抛物线的两条切线，切点分别为，且切点弦恒过点.

    （1）求和；

    （2）求证：动点在一条定直线上运动.

    【答案】（1），.（2）证明见解析

    【解析】

    （1）根据抛物线的定义求得，由此求得抛物线方程，将的坐标代入抛物线方程，由此求得.

    （2）设出的坐标，根据抛物线的切线方程求得直线的方程，将的坐标代入直线的方程，由此求得直线的方程，将点坐标代入直线的方程，由此判断出动点在直线上运动.

    （1）由题意得

    抛物线方程为，∴，

    （2）首先推导抛物线切线方程的一般性：设抛物线上的一点为，由，所以抛物线过点的切线的斜率为，切线方程为，化简得.

    设

    ∴抛物线的切线的方程：

    抛物线的切线的方程：

    ∵均经过，∴

    故直线即过，也过

    故方程：

    ∵它恒过，∴，∴它在上运动.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

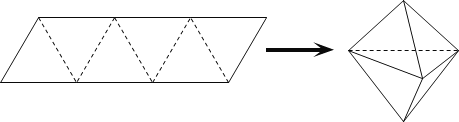
    【题目】农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，俗称“粽子”，古称“角黍”，是端午节大家都会品尝的食品，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的体积为____；若该六面体内有一球，则该球体积的最大值为____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某社区消费者协会为了解本社区居民网购消费情况，随机抽取了100位居民作为样本，就最近一年来网购消费金额（单位：千元），网购次数和支付方式等进行了问卷调查．经统计这100位居民的网购消费金额均在区间内，按分成6组，其频率分布直方图如图所示．

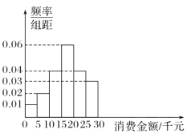
    （1）估计该社区居民最近一年来网购消费金额的中位数；

    （2）将网购消费金额在20千元以上者称为“网购迷”，补全下面的列联表，并判断有多大把握认为“网购迷与性别有关系”

    男

    女

    总计

    网购迷

    20

    非网购迷

    45

    总计

    100

    附：．

    临界值表：

    0.01

    0.05

    0.025

    0.010

    0.005

    0.001

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某运动制衣品牌为了成衣尺寸更精准，现选择15名志愿者，对其身高和臂展进行测量（单位：厘米），左图为选取的15名志愿者身高与臂展的折线图，右图为身高与臂展所对应的散点图，并求得其回归方程为，以下结论中不正确的为

    A. 15名志愿者身高的极差小于臂展的极差

    B. 15名志愿者身高和臂展成正相关关系，

    C. 可估计身高为190厘米的人臂展大约为189.65厘米，

    D. 身高相差10厘米的两人臂展都相差11.6厘米，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体中，分别为的中点.

    （1）求证：平面；

    （2）求证：平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体ABCD﹣HKLE中，底面ABCD是边长为3的正方形，对角线AC与BD相交于点O，点F在线段AH上且，BE与底面ABCD所成角为.

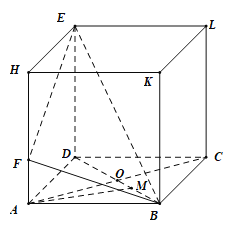
    （1）求证：AC⊥BE；

    （2）M为线段BD上一点，且，求异面直线AM与BF所成角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点F是拋物线C:y2=2px(p>0)的焦点,点M(x0,1)在C上,且|MF|=.

    (1)求p的值;

    (2)若直线l经过点Q(3,-1)且与C交于A,B(异于M)两点,证明:直线AM与直线BM的斜率之积为常数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，若关于的方程恰有三个不相等的实数解，则的取值范围是　　

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调区间情况；

    （2）若函数有且只有两个零点，证明：.

    查看答案和解析>>

    同步练习册答案