练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知点为圆上一动点，轴于点，若动点满足（其中为非零常数）

    （1）求动点的轨迹方程；

    （2）当时，得到动点的轨迹为曲线，斜率为1的直线与曲线相交于，两点，求面积的最大值.

    【答案】（1）（2）

    【解析】试题分析：（1）根据条件用Q点坐标表示A点坐标，再代入化简可得的轨迹方程；（2）设直线的方程为，根据点到直线距离公式可得三角形的高，联立直线方程与椭圆方程，利用韦达定理及弦长公式可得三角形底边边长，再根据三角形面积公式可得，最后根据基本不等式求最大值

    试题解析：解：（Ⅰ）设动点，则，且，①

    又，得，

    代入①得动点的轨迹方程为．

    （Ⅱ）当时，动点的轨迹曲线为．

    设直线的方程为，代入中，

    得，

    由，∴，

    设，，

    ∵点到直线的距离，，

    ，

    当且仅当，即时取到最大值．

    ∴面积的最大值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20,30），[30,40），┄，[80,90]，并整理得到如下频率分布直方图：

    （Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；

    （Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；

    （Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知7cos2α﹣sinαcosα﹣1=0，α∈（ ， ），求cos2α和 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得 M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°．已知山高BC=100m，则山高MN=m．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x），g（x）都是定义在R上的函数，且满足以下条件：
    ①f（x）=axg（x）（a＞0，a≠1）；
    ②g（x）≠0；
    ③f（x）g'（x）＞f'（x）g（x）；
    若 ，则a= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：函数 在（﹣∞，+∞）上有极值，命题q：双曲线 的离心率e∈（1，2）．若p∨q是真命题，p∧q是假命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为考察高中生的性别与是否喜欢数学课程之间的关系，在某城市的某校高中生中，从男生中随机抽取了70人，从女生中随机抽取了50人，男生中喜欢数学课程的占，女生中喜欢数学课程的占，得到如下列联表.

    喜欢数学课程

    不喜欢数学课程

    合计

    男生

    女生

    合计

    （1）请将列联表补充完整；试判断能否有90%的把握认为喜欢数学课程与否与性别有关；

    （2）从不喜欢数学课程的学生中采用分层抽样的方法，随机抽取6人，现从6人中随机抽取2人，求抽取的学生中至少有1名是女生的概率..

    附：，其中.

    0.150

    0.100

    0.050

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，椭圆C： (a＞b＞0)的离心率为，且过点(1， )．过椭圆C的左顶点A作直线交椭圆C于另一点P，交直线l：x＝m(m＞a)于点M．已知点B(1，0)，直线PB交l于点N．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）若MB是线段PN的垂直平分线，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点为抛物线的焦点，点在抛物线上，且．

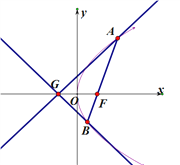
    （1）求抛物线的方程；

    （2）已知点，延长交抛物线于点，证明：以点为圆心且与直线相切的圆，必与直线相切．

    查看答案和解析>>

    同步练习册答案