
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值集合;
的取值集合;
(2)在函数![]() 的图像上取定点
的图像上取定点![]() ,记直线AB的斜率为K,证明:存在
,记直线AB的斜率为K,证明:存在![]() ,使
,使![]() 恒成立;
恒成立;
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)对一切x>0,f(x)≤![]() 恒成立,即对一切x>0,
恒成立,即对一切x>0,![]() 恒成立,构造新函数,求出函数的最值,即可求得结论;
恒成立,构造新函数,求出函数的最值,即可求得结论;
(2)要证明存在x0∈(x1,x2),使f′(x0)=k成立,只要证明f′(x)﹣k=0在(x1,x2)内有解即可.
(1)解:对一切x>0,f(x)≤![]() 恒成立,
恒成立,
即对一切x>0,![]() 恒成立,
恒成立,
令![]() ,则
,则![]()
令g′(x)>0,可得0<x<![]() ;令g′(x)<0,可得x>
;令g′(x)<0,可得x>![]() ,
,
∴x=![]() 时,g(x)取得最大值g(
时,g(x)取得最大值g(![]() )
)![]()
∴![]() ;
;
令![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递减,在在
上单调递减,在在![]() 上单调递增,
上单调递增,
∴![]() ,又
,又![]() ,
,
∴![]()
∴![]() 的取值集合
的取值集合![]() ;
;
(2)证明:由题意,k![]()
要证明存在x0∈(x1,x2),使f′(x0)=k成立,只要证明f′(x)﹣k=0在(x1,x2)内有解即可
令h(x)=f′(x)﹣k![]() ,只要证明h(x)在(x1,x2)内存在零点即可
,只要证明h(x)在(x1,x2)内存在零点即可
∵h(x)在(x1,x2)内是减函数,只要证明h(x1)>0,h(x2)<0
即证![]() 0,
0,![]() 0
0
令F(t)=t﹣1﹣lnt(t>0),∵F′(t)=1![]() ,∴函数在(0,1)上单调递减,在(1,+∞)上单调递增
,∴函数在(0,1)上单调递减,在(1,+∞)上单调递增
∴函数在t=1时,取得最小值0,∴F(t)≥0
∵![]() 0且
0且![]() ;
;![]() 0且
0且![]() 1
1
∴![]() 0,
0,![]() 0
0
∴结论成立.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
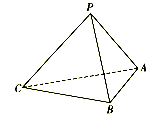
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长四尺,莞生一日,长一尺.蒲生日自半,莞生日自倍.意思是:今有蒲第一天长高四尺,莞第一天长高一尺,以后蒲每天长高前一天的一半,莞每天长高前一天的两倍.请问第几天,莞的长度是蒲的长度的4倍( )
A.4天B.5天C.6天D.7天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来就一直使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字开始,“地支”以“子”字开始,两者按照干支顺序相配,构成了“干支纪年法”,其相配顺序为:甲子、乙丑、丙寅![]() 癸酉、甲戌、乙亥、丙子
癸酉、甲戌、乙亥、丙子![]() 癸未、甲申、乙酉、丙戌
癸未、甲申、乙酉、丙戌![]() 癸巳
癸巳![]() 癸亥,60为一个周期,周而复始,循环记录.按照“干支纪年法”,中华人民共和国成立的那年为己丑年,则2013年为( )
癸亥,60为一个周期,周而复始,循环记录.按照“干支纪年法”,中华人民共和国成立的那年为己丑年,则2013年为( )
A.甲巳年B.壬辰年C.癸巳年D.辛卯年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给正有理数![]() 、
、![]() (
(![]() ,
,![]() ,
,![]() ,且
,且![]() 和
和![]() 不同时成立),按以下规则
不同时成立),按以下规则![]() 排列:① 若
排列:① 若![]() ,则
,则![]() 排在
排在![]() 前面;② 若
前面;② 若![]() ,且
,且![]() ,则
,则![]() 排在
排在![]() 的前面,按此规则排列得到数列
的前面,按此规则排列得到数列![]() .
.
(例如:![]() ).
).
(1)依次写出数列![]() 的前10项;
的前10项;
(2)对数列![]() 中小于1的各项,按以下规则
中小于1的各项,按以下规则![]() 排列:①各项不做化简运算;②分母小的项排在前面;③分母相同的两项,分子小的项排在前面,得到数列
排列:①各项不做化简运算;②分母小的项排在前面;③分母相同的两项,分子小的项排在前面,得到数列![]() ,求数列
,求数列![]() 的前10项的和
的前10项的和![]() ,前2019项的和
,前2019项的和![]() ;
;
(3)对数列![]() 中所有整数项,由小到大取前2019个互不相等的整数项构成集合
中所有整数项,由小到大取前2019个互不相等的整数项构成集合![]() ,
,![]() 的子集
的子集![]() 满足:对任意的
满足:对任意的![]() ,有
,有![]() ,求集合
,求集合![]() 中元素个数的最大值.
中元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拥有3条相同的生产线,每条生产线每月至多出现一次故障.各条生产线是否出现故障相互独立,且出现故障的概率为![]() .
.
(1)求该企业每月有且只有1条生产线出现故障的概率;
(2)为提高生产效益,该企业决定招聘名维修工人及时对出现故障的生产线进行维修.已知每名维修工人每月只有及时维修1条生产线的能力,且每月固定工资为1万元.此外,统计表明,每月在不出故障的情况下,每条生产线创造12万元的利润;如果出现故障能及时维修,每条生产线创造8万元的利润;如果出现故障不能及时维修,该生产线将不创造利润,以该企业每月实际获利的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
之中选其一,应选用哪个?(实际获利=生产线创造利润-维修工人工资)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com