
【题目】当![]() ,则称点
,则称点![]() 为平面上单调格点:设
为平面上单调格点:设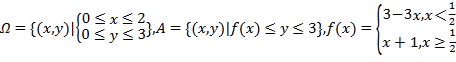
求从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上的概率;
上的概率;
求从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点的概率.
上的格点的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)作出集合![]() 所对应的区域,记事件
所对应的区域,记事件![]() “从区域
“从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上”,根据几何概型,利用面积比,即可求解概率;
上”,根据几何概型,利用面积比,即可求解概率;
(2)事件![]() “从区域
“从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点”,得出基本事件的总数,和事件
上的格点”,得出基本事件的总数,和事件![]() 所包含的基本事件的个数,利用古典概型及概率的计算公式,即可求解事件的概率.
所包含的基本事件的个数,利用古典概型及概率的计算公式,即可求解事件的概率.
试题解析:
作出集合![]() 所对应的区域(如图):
所对应的区域(如图):
矩形![]()
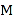
则:(1)记事件![]() “从区域
“从区域![]() 中任取一点
中任取一点![]() ,而该点落在区域
,而该点落在区域![]() 上”
上”
则事件![]() 符合几何概型,即
符合几何概型,即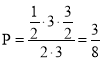 .
.
(2)事件![]() “从区域
“从区域![]() 中的所有格点中任取一点
中的所有格点中任取一点![]() ,而该点是区域
,而该点是区域![]() 上的格点”
上的格点”
则事件![]() 符合古典概型,区域
符合古典概型,区域![]() 中的格点个数:当横坐标分别为0,1,2时,纵坐标可以为0,1,2,3中的任一个,此时有
中的格点个数:当横坐标分别为0,1,2时,纵坐标可以为0,1,2,3中的任一个,此时有![]() 个;而区域
个;而区域![]() 上的格点有(0,3),(1,2),(2,3),(1,2)共4个,
上的格点有(0,3),(1,2),(2,3),(1,2)共4个,
∴![]()


科目:高中数学 来源: 题型:
【题目】已知△ABC中,A,B,C的对边分别是a,b,c,且2cos2 ![]() sinB,a=3c
sinB,a=3c
(Ⅰ)分别求tanC和sin2C的值;
(Ⅱ)若b=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和Sn , 首项a1=a,公比为q(q≠0且q≠1).
(1)推导证明:Sn= ![]() ;
;
(2)等比数列{an}中,是否存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列?若存在,求出符合条件的等比数列公比q的值,若不存在,说明理由;
(3)本题中,若a=q=2,已知数列{nan}的前n项和Tn , 是否存在正整数n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的角A、B、C所对的边分别是a、b、c,设向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求证:△ABC为等腰三角形;
,求证:△ABC为等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,边长c=2,角C=
,边长c=2,角C= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:
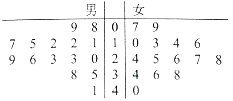
若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人?
(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人,参加读书日宣传活动.
(i)共有多少种不同的抽取方法?
(ii)求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com