
已知函数 :
:
(1)若函数在区间 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;
(2)问:是否存在常数 ,当
,当 时,
时, 的值域为区间
的值域为区间 ,且
,且 的长度为
的长度为 .
.
(1) 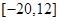 ;(2)存在,见解析.
;(2)存在,见解析.
【解析】
试题分析:(1) 先由函数对称轴为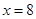 得函数在
得函数在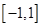 上单调减,要使函数在
上单调减,要使函数在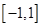 存在零点,则需满足
存在零点,则需满足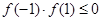 ,解得
,解得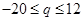 ; (2)当
; (2)当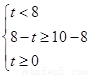 时,
时,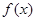 的值域为
的值域为 ,由
,由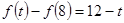 ,得
,得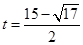 合题意;当
合题意;当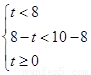 时,
时,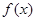 的值域为
的值域为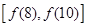 ,由
,由 ,得不合题意;当
,得不合题意;当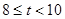 时,
时,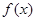 的值域为
的值域为 ,用上面的方法得
,用上面的方法得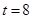 或
或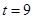 合题意.
合题意.
试题解析:⑴ ∵二次函数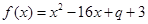 的对称轴是
的对称轴是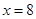
∴函数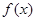 在区间
在区间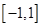 上单调递减
上单调递减
∴要函数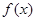 在区间
在区间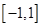 上存在零点须满足
上存在零点须满足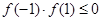
即 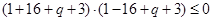
解得 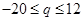 ,所以
,所以 .
.
⑵ 当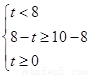 时,即
时,即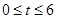 时,
时,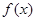 的值域为:
的值域为: ,即
,即 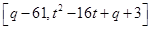
∴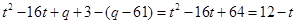
∴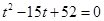 ∴
∴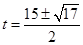
经检验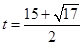 不合题意,舍去。
不合题意,舍去。
当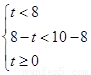 时,即
时,即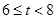 时,
时,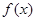 的值域为:
的值域为: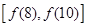 ,即
,即 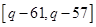
∴ , ∴
, ∴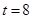
经检验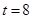 不合题意,舍去。
不合题意,舍去。
当
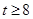 时,
时,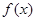 的值域为:
的值域为: ,即
,即 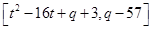
∴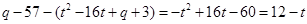
∴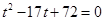 ∴
∴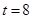 或
或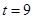
经检验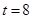 或
或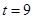 或
或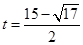 满足题意。
满足题意。
所以存在常数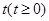 ,当
,当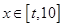 时,
时,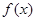 的值域为区间
的值域为区间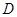 ,且
,且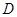 的长度为
的长度为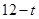 .
.
考点:零点存在性定理、二次函数的单调性、二次函数值域、分类讨论思想.


科目:高中数学 来源:2010年重庆市高二上学期期中考试理科数学卷 题型:解答题
(本小题满分12分)
已知函数 ,
,
(1)
若 ,
, ,且
,且 的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点(
的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点( ),设直线PQ的斜率为k,求证:
),设直线PQ的斜率为k,求证: ;
;
(2) 若 ,且
,且 的定义域是
的定义域是 ,
, .
.
求证: .
.
查看答案和解析>>
科目:高中数学 来源:重庆市2009-2010学年度下期期末考试高二数学试题(文科) 题型:解答题
1. (本小题满分13分)
已知函数 .
.
(1)
若 在x = 0处取得极值为 – 2,求a、b的值;
在x = 0处取得极值为 – 2,求a、b的值;
(2)
若 在
在 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com