
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
【答案】D
【解析】解:当k=0,S=a0时,满足进行循环的条件,执行循环体后,k=1,S=a0x+a1 ,
当k=1,S=a0x+a1时,满足进行循环的条件,执行循环体后,k=2,S=a0x2+a1x+a2 ,
当k=2,S=a0x2+a1x+a2时,满足进行循环的条件,执行循环体后,k=3,S=a0x3+a1x2+a2x+a3 ,
当k=3,S=a0x3+a1x2+a2x+a3时,不满足进行循环的条件,
故输出结果为:a0x3+a1x2+a2x+a3 ,
故选:D
【考点精析】利用程序框图对题目进行判断即可得到答案,需要熟知程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,F为椭圆E:![]() 的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D.
的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D.
(1)当AB=![]() 时,求直线AB的方程;
时,求直线AB的方程;
(2)直线AB交直线x=3于点M,OM与CD交于P,CO与椭圆E交于Q,求证:OM∥DQ.
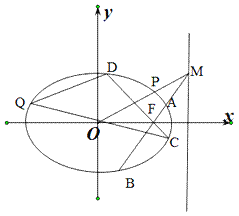
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ax2+ ![]() .
.
(I) 当a= ![]() 时,判断f(x)在其定义上的单调性;
时,判断f(x)在其定义上的单调性;
(Ⅱ)若函数f(x)有两个极值点x1 , x2 , 其中x1<x2 . 求证:
(i)f(x2)>0;
(ii)x1+x2> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x+ ![]() +1(a∈R).
+1(a∈R).
(1)讨论f(x)的单调性与极值点的个数;
(2)当a=0时,关于x的方程f(x)=m(m∈R)有2个不同的实数根x1 , x2 , 证明:x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
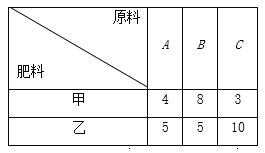
现有A种原料200吨,B种原料360吨,C种原料300吨.在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级实行选课走班教学,学校为学生提供了多种课程,其中数学科提供5种不同层次的课程,分别称为数学1、数学2、数学3、数学4、数学5,每个学生只能从这5种数学课程中选择一种学习,该校高二年级1800名学生的数学选课人数统计如表:
课程 | 数学1 | 数学2 | 数学3 | 数学4 | 数学5 | 合计 |
选课人数 | 180 | 540 | 540 | 360 | 180 | 1800 |
为了了解数学成绩与学生选课情况之间的关系,用分层抽样的方法从这1800名学生中抽取了10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少有2人选择数学2的概率;
(2)从选出的10名学生中随机抽取3人,记这3人中选择数学2的人数为X,选择数学1的人数为Y,设随机变量ξ=X﹣Y,求随机变量ξ的分布列和数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+2a2+3a3+…+nan=n(n∈N*).
(1)求数列{an}的通项公式an;
(2)令 ![]() ,写出Tn关于n的表达式,并求满足Tn>
,写出Tn关于n的表达式,并求满足Tn> ![]() 时n的取值范围.
时n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com