甲盒中有黑、白两种颜色的球各2个;乙盒中有黄、黑、白三种颜色的球各1个.
(1)从两个盒子中各取1个球,求取出的两个球是不同颜色的概率;
(2)若把两盒中的球混到一起,从中不放回的先后取两球,求取出的两个球是不同颜色的概率.
解:(1)取出的两球是不同颜色的对立事件是取出的两球是相同颜色,
取出的两球是相同颜色包含取出的两球都是白色,都是黑色,这两种情况是互斥的,
当两个盒子都取出的是黑色的概率是
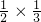
=

,
当两个盒子取出的球都是白色的概率是
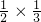
=

∴取出的球颜色相同的概率是
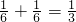
∴取出的球颜色不同的概率是1-

=

.
(2)取出的两球是不同颜色的对立事件是取出的两球是相同颜色,
取出的两球是相同颜色包含取出的两球都是白色,都是黑色,这两种情况是互斥的,
两次都取得颜色相同的球的概率是
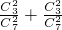
=

,
∴取出的两个球是不同颜色的概率是1-

=

即取出的两个球颜色不同的概率是

分析:(1)取出的两球是不同颜色的对立事件是取出的两球是相同颜色,取出的两球是相同颜色包含取出的两球都是白色,都是黑色,写出事件包含的基本事件数,得到概率,根据对立事件的概率得到最后结果.
(2)取出的两球是不同颜色的对立事件是取出的两球是相同颜色,取出的两球是相同颜色包含取出的两球都是白色,都是黑色,这两种情况是互斥的,做出取出球的颜色相同的概率.利用对立事件的概率得到结果.
点评:本题是一个等可能事件的概率问题,考查对立事件的概率,对立事件是指同一次试验中,不会同时发生的事件,解题时往往先求它的对立事件的概率.

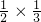 =
= ,
,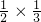 =
=
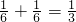
 =
= .
.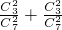 =
= ,
, =
=



 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案