【题目】已知在等比数列{an}中，a1=1，且a2是a1和a3﹣1的等差中项．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=2n﹣1+an（n∈N*），求{bn}的前n项和Sn ．
【答案】
（1）解：设等比数列{an}的公比为q，
∵a2是a1和a3﹣1的等差中项，a1=1，
∴2a2=a1+（a3﹣1）=a3，
∴ 
=2，
∴ 
=2n﹣1，（n∈N*）．
（2）解：∵bn=2n﹣1+an，
∴ 
（2n﹣1+2n﹣1）
=[1+3+5+…+（2n﹣1）]+（1+2+22+…+2n﹣1）
= 
+ 
=n2+2n﹣1．
【解析】（1）设等比数列{an}的公比为q，由a2是a1和a3﹣1的等差中项，a1=1，知2a2=a1+（a3﹣1）=a3 ， 由此能求出数列{an}的通项公式．．（2）由bn=2n﹣1+an ， 知 （2n﹣1+2n﹣1）=[1+3+5+…+（2n﹣1）]+（1+2+22+…+2n﹣1），由等差数列和等比数列的求和公式能求出Sn ．
科目：高中数学 来源： 题型：
【题目】如图所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中点． 
（1）求证：平面CFM⊥平面BDF；
（2）点N在CE上，EC=2，FD=3，当CN为何值时，MN∥平面BEF．
查看答案和解析>>
科目：高中数学 来源： 题型：
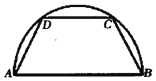
【题目】如图，将一半径为2的半圆形纸板裁剪成等腰梯形ABCD的形状，下底AB是半圆的直径，上底CD的端点在圆周上，则所得梯形面积的最大值为（ ）
A. 3
B. 3
C. 5
D. 5
查看答案和解析>>
科目：高中数学 来源： 题型：
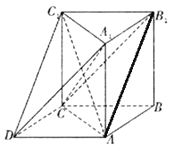
【题目】如下图所示的几何体中， 
为三棱柱，且
，四边形
为平行四边形， 
， 
.
（1）求证： 
；
（2）若
，求证： 
；
（3）若
，二面角
的余弦值为若
，求三棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四边形ABCD中， 
=（2，﹣2）， 
=（x，y）， 
=（1， 
）．
（1）若 ∥ 
，求x，y之间的关系式；
（2）满足（1）的同时又有 
⊥ 
，求x，y的值以及四边形ABCD的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=lg（x2+tx+2）（t为常数，且﹣2 
＜t＜2 ）．
（1）当x∈[0，2]时，求函数f（x）的最小值（用t表示）；
（2）是否存在不同的实数a，b，使得f（a）=lga，f（b）=lgb，并且a，b∈（0，2）．若存在，求出实数t的取值范围；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
，满足
，
．数列
满足
，，且
．
（1）求数列和的通项公式；
（2）若
，数列
的前项和为
，对任意的，都有
，求实数
的取值范围；
（3）是否存在正整数
，，使
，
，
（
）成等差数列，若存在，求出所有满足条件的，，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（1，sinx）， 
=（cos（2x+ 
），sinx），函数f（x）= ﹣ 
cos2x
（1）求函数f（x）的解析式及其单调递增区间；
（2）当x∈[0， ]时，求函数f（x）的值域．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
