
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.

(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
【答案】(1)![]() ;(2)当
;(2)当![]() 时,甲、乙两游客距离最短;(3)
时,甲、乙两游客距离最短;(3)![]() .
.
【解析】
试题分析:(1)根据两角和公式求得![]() ,再根据正弦定理即可求得
,再根据正弦定理即可求得![]() 的长;(2)假设乙出发
的长;(2)假设乙出发![]() 后,甲、乙两游客距离为
后,甲、乙两游客距离为![]() ,分别表示出甲、乙二人行走的距离,根据余弦定理建立
,分别表示出甲、乙二人行走的距离,根据余弦定理建立![]() 的二次函数关系,求出使得甲乙二人距离最短时
的二次函数关系,求出使得甲乙二人距离最短时![]() 的值;(3)根据正弦定理求得
的值;(3)根据正弦定理求得![]() ,乙从
,乙从![]() 出发时,甲已走了
出发时,甲已走了![]()
![]() ,还需走710
,还需走710![]() 才能到达
才能到达![]() ,设乙步行的速度为
,设乙步行的速度为![]() ,由题意得
,由题意得![]() ,J解不等式即可求得乙步行速度的范围.
,J解不等式即可求得乙步行速度的范围.
试题解析:(1)在![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
从而![]()
![]()
![]() .
.
由正弦定理![]() ,得
,得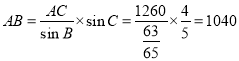 (
(![]() ).
).
(2)假设乙出发![]() 后,甲、乙两游客距离为
后,甲、乙两游客距离为![]() ,此时,甲行走了
,此时,甲行走了![]() ,乙距离
,乙距离![]() 处
处![]()
![]() ,
,
所以由余弦定理得![]()
![]() ,
,
由于![]() ,即
,即![]() ,
,
故当![]() 时,甲、乙两游客距离最短.
时,甲、乙两游客距离最短.
(3)由正弦定理![]() ,
,
得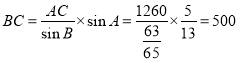 (
(![]() ).
).
乙从![]() 出发时,甲已走了
出发时,甲已走了![]() (
(![]() ),还需走710
),还需走710![]() 才能到达
才能到达![]() .
.
设乙步行的速度为![]() ,由题意得
,由题意得![]() ,解得
,解得![]() ,
,
所以为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在
,乙步行的速度应控制在![]() (单位:
(单位:![]() )范围内.
)范围内.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,左、右焦点
的中心在坐标原点,左、右焦点![]() 分别在
分别在![]() 轴上,离心率为
轴上,离心率为![]() ,在其上有一动点
,在其上有一动点![]() ,
,![]() 到点
到点![]() 距离的最小值是1.过
距离的最小值是1.过![]() 作一个平行四边形,顶点
作一个平行四边形,顶点![]() 都在椭圆
都在椭圆![]() 上,如图所示.
上,如图所示.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)判断![]() 能否为菱形,并说明理由.
能否为菱形,并说明理由.
(Ⅲ)当![]() 的面积取到最大值时,判断
的面积取到最大值时,判断![]() 的形状,并求出其最大值.
的形状,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,
,![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数字0、2、3、4、6按下列要求组数、计算:
(1)能组成多少个没有重复数字的三位数?
(2)可以组成多少个可以被3整除的没有重复数字的三位数?
(3)求![]() 即144的所有正约数的和.
即144的所有正约数的和.
(注:每小题结果都写成数据形式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为![]() ;小李后掷一枚骰子,向上的点数记为
;小李后掷一枚骰子,向上的点数记为![]() .
.
(1)求![]() 能被
能被![]() 整除的概率.
整除的概率.
(2)规定:若![]() ,则小王赢;若
,则小王赢;若![]() ,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
,则小李赢,其他情况不分输赢.试问这个游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五面体![]() 中,
中,![]() ,底面
,底面![]() 是正三角形,
是正三角形,![]() ,四边形
,四边形![]() 是矩形,二面角
是矩形,二面角![]() 为直二面角.
为直二面角.
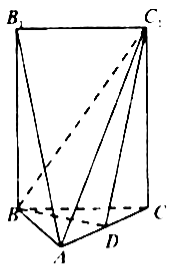
(1)![]() 在
在![]() 上运动,当
上运动,当![]() 在何处时,有
在何处时,有![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 余弦值.
余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com