
【题目】在△ABC中,a,b,c分别是内角A,B,C的对边,且(a+c)2=b2+3ac
(Ⅰ)求角B的大小;
(Ⅱ)若b=2,且sinB+sin(C﹣A)=2sin2A,求△ABC的面积.
【答案】解:(Ⅰ) 把(a+c)2=b2+3ac整理得,a2+c2﹣b2=ac,
由余弦定理有cosB= ![]() =
= ![]() =
= ![]() ,
,
∵B为三角形内角,
∴B= ![]() ;
;
(Ⅱ)在△ABC中,A+B+C=π,即B=π﹣(A+C),
∴sinB=sin(A+C),
由已知sinB+sin(C﹣A)=2sin2A可得:sin(A+C)+sin(C﹣A)=4sinAcosA,
∴sinAcosC+cosAsinC+sinCcosA﹣cosCsinA=4sinAcosA,
整理得:cosAsinC=2sinAcosA,
若cosA=0,则A= ![]() ,于是由b=2,可得c=
,于是由b=2,可得c= ![]() =
= ![]() ,
,
此时△ABC的面积为S= ![]() bc=
bc= ![]() ;
;
若cosA≠0,则sinC=2sinA,由正弦定理可知,c=2a,
代入a2+c2﹣b2=ac整理可得:3a2=4,
解得:a= ![]() ,进而c=
,进而c= ![]() ,
,
此时△ABC的面积S= ![]() acsinB=
acsinB= ![]() ,
,
∴综上所述,△ABC的面积为 ![]() .
.
【解析】(1)把(a+c)2=b2+3ac整理得,a2+c2﹣b2=ac,根据余弦定理可得cosB的值,不难得出B的角度,(2)由三角形三内角和为π,可得sinB=sin(A+C),由已知sinB+sin(C﹣A)=2sin2A可得:sin(A+C)+sin(C﹣A)=4sinAcosA,根据两角和与差的正弦公式进行整理得:cosAsinC=2sinAcosA,分类讨论当cosA=0和cosA≠0分别求得△ABC的面积.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() ,以及对余弦定理的定义的理解,了解余弦定理:
,以及对余弦定理的定义的理解,了解余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R.
(1)若a=0时,求函数y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣f'(0)ex+2x,点P为曲线y=f(x)在点(0,f(0))处的切线l上的一点,点Q在曲线y=ex上,则|PQ|的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游公司为甲,乙两个旅游团提供四条不同的旅游线路,每个旅游团可任选其中一条旅游线路.
(1)求甲、乙两个旅游团所选旅游线路不同的概率;
(2)某天上午9时至10时,甲,乙两个旅游团都到同一个著名景点游览,20分钟后游览结束即离去.求两个旅游团在该著名景点相遇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax﹣lnx,a∈R.
(1)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(2)令g(x)=f(x)﹣x2 , 是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(3)求证:当x∈(0,e]时,e2x2﹣ ![]() x>(x+1)lnx.
x>(x+1)lnx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上的一点A(2,4).
(Ⅰ)是否存在直线l:y=kx+3与圆M有两个交点B,C,并且|AB|=|AC|,若有,求此直线方程,若没有,请说明理由;
(Ⅱ)设点T(t,0)满足:存在圆M上的两点P和Q,使得 ![]() =
= ![]() ,求实数t的取值范围.
,求实数t的取值范围.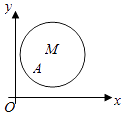
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C依次成等差数列,其对边分别为a,b,c,且b= ![]() asinB.
asinB.
(1)求内角C;
(2)若b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com