
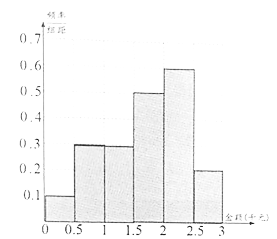
【题目】某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):

若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3:2.
(1)试确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定5人,若需从这5人中随机选取2人进行问卷调查,则恰好选取1名“网购达人”和1名“非网购达人”的概率是多少?
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)由总人数和“非网购达人”与“网购达人”人数比可列出关于![]() 的方程组,从而解得
的方程组,从而解得![]() ,也即可计算出其频率
,也即可计算出其频率![]() ;
;
(2)5人中有3人是“非网购达人”,有2人是“网购达人”,把他们编号(两者可用不同符号),用列举法列出任选2的所有组合,从中可得恰好选取1名“网购达人”和1名“非网购达人”的选法,最后可得概率.
试题解析:
(1)根据题意,有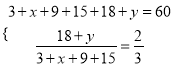 ,解得
,解得![]() ,∴
,∴![]() ,
, ![]()
补全频率分布直方图如图所示.
(2)用分层抽样的方法,从中选取5人,则其中“网购达人”有![]() 人,“非网购达人”有
人,“非网购达人”有![]() 人,设“网购达人”编号为1、2,“非网购达人”编号为3、4、5,
人,设“网购达人”编号为1、2,“非网购达人”编号为3、4、5,
则基本事件空间![]() ,
,
其中基本事件的个数为10,
事件![]() “恰好选取1名‘网购达人’和1名‘非网购达人’”
“恰好选取1名‘网购达人’和1名‘非网购达人’” ![]()
![]()
其中基本事件的个数为6,则![]() ,即恰好选取1名“网购达人”和1名“非网购达人”的概率为
,即恰好选取1名“网购达人”和1名“非网购达人”的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.

(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试的平均分;
(3)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,且将全班25人的成绩记为![]() 由右边的程序运行后,输出
由右边的程序运行后,输出![]() .据此解答如下问题:
.据此解答如下问题:
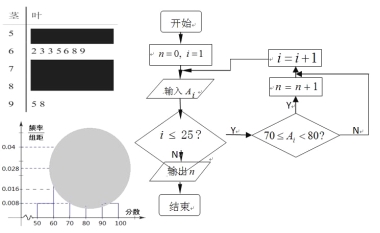
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两艘轮船都要停靠在同一个泊位,它们可能在一昼夜的任意时刻到达.甲、乙两船停靠泊位的时间分别为4小时与2小时,求有一艘船停靠泊位时必需等待一段时间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各种情况下,向量终点构成什么图形?
(1)把所有单位向量的起点平移到同一点![]() ;
;
(2)把平行于某一直线的所有单位向量的起点平移到同一点;
(3)把平行于某一直线的一切向量平移到同一起点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:22,23,25,26,31,30;若B样本数据恰好是A样本中每个数据都减去10后所得的数据,则A,B两样本的下列数字特征相同的是( )
A.方差B.平均数C.众数D.中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com