
【题目】如图1,梯形![]() 中,
中,![]() ,过
,过![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.![]() ,
,![]() ,已知
,已知![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2.
,如图2.
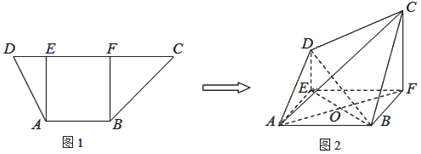
(1)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(2)在(1)的条件下,若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证![]() 平面
平面![]() ,得到
,得到![]() ,结合
,结合![]() ,可证得
,可证得![]() 平面
平面![]() ;
;
(2)以![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,求出面ADF与面ACF的法向量,利用夹角公式,求出两法向量夹角的余弦值,由图可知二面角
轴的正方向建立空间直角坐标系,求出面ADF与面ACF的法向量,利用夹角公式,求出两法向量夹角的余弦值,由图可知二面角![]() 为锐角,则它的余弦值为正值,即可得到本题答案.
为锐角,则它的余弦值为正值,即可得到本题答案.
(1)由已知得四边形![]() 是正方形,且边长为2,
是正方形,且边长为2,
在图2中,![]() ,由已知得
,由已知得![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)在图2中,由(1)知![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,
轴的正方向建立空间直角坐标系,
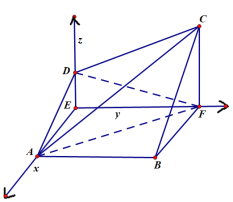
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由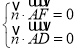 得
得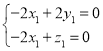 ,不妨取
,不妨取![]() ,得
,得![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由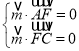 得
得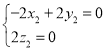 ,取
,取![]() ,得
,得![]() ,
,
![]()
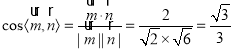 .
.
由图可得,二面角![]() 为锐角,所以它的余弦值为
为锐角,所以它的余弦值为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,△
为正方形,△![]() 为等边三角形,
为等边三角形,![]() 是
是![]() 中点,平面
中点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(III)记四棱锥![]() 的体积为
的体积为![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,直接写出
,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,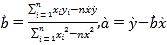 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共![]() 层,总开发费用为
层,总开发费用为![]() 万元,求函数
万元,求函数![]() 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着通识教育理念的推广及高校课程改革的深入,选修课越来越受到人们的重视.国内一些知名院校在公共选修课的设置方面做了许多有益的探索,并且取得了一定的成果.因为选修课的课程建设处于探索阶段,选修课的教学、管理还存在很多的问题,所以需要在通识教育的基础上制定科学的、可行的解决方案,为学校选修课程的改革与创新、课程设置、考试考核、人才培养提供参考.某高校采用分层抽样法抽取了数学专业的50名参加选修课与不参加选修课的学生的成绩,统计数据如下表:
成绩优秀 | 成绩不够优秀 | 总计 | |
参加选修课 | 16 | 9 | 25 |
不参加选修课 | 8 | 17 | 25 |
总计 | 24 | 26 | 50 |
(1)试运用独立性检验的思想方法你能否有99%的把握认为“学生的成绩优秀与是否参加选修课有关”,并说明理由;
(2)如果从数学专业随机抽取5名学生,求抽到参加选修课的学生人数![]() 的分布列和数学期望(将频率当做概率计算).
的分布列和数学期望(将频率当做概率计算).
参考公式: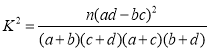 ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数 ,下列
,下列![]() 个结论正确的是__________(把你认为正确的答案全部写上).
个结论正确的是__________(把你认为正确的答案全部写上).
(1)任取![]() ,都有
,都有![]() ;
;
(2)函数![]() 在
在![]() 上单调递增;
上单调递增;
(3)![]() ,对一切
,对一切![]() 恒成立;
恒成立;
(4)函数![]() 有
有![]() 个零点;
个零点;
(5)若关于![]() 的方程
的方程![]() 有且只有两个不同的实根
有且只有两个不同的实根![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com