在平面直角坐标系xOy中.已知点A.P是动点.且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA．求点P的轨迹方程．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

11．在平面直角坐标系xOy中，已知点A（-1，1），P是动点，且三角形POA的三边所在直线的斜率满足k_OP+k_OA=k_PA．求点P的轨迹方程．

分析设点P（x，y）．由于k_OP+k_OA=k_PA，利用斜率计算公式可得$\frac{y}{x}+（-1）=\frac{y-1}{x+1}$，化简即为点P的轨迹方程．

解答解：设点P（x，y）为所求轨迹上的任意一点，
则由k_OP+k_OA=k_PA，得$\frac{y}{x}+（-1）=\frac{y-1}{x+1}$，
整理得轨迹C的方程为y=x²（x≠0且x≠-1）．

点评本题考查轨迹方程的求法，考查运算求解能力，推理论证能力，比较基础．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

1．

如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，此时气球的高是30m，则河流的宽度BC等于（　　）

A．

$30（\sqrt{3}-1）m$

B．

$60（\sqrt{3}-1）m$

C．

$90（\sqrt{3}-1）m$

D．

$120（\sqrt{3}-1）m$

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

2．在同一坐标系中，曲线$\frac{x^2}{16}+\frac{y^2}{9}$=1经过伸缩变换$\left\{\begin{array}{l}{x^'}=\frac{1}{4}x\\{y^'}=\frac{1}{3}y\end{array}$后，得到的曲线的方程是（　　）

A．

$\frac{{{x^'}^2}}{4}+\frac{{{y^'}^2}}{3}=1$

B．

$\frac{{{y^'}^2}}{4}+\frac{{{x^'}^2}}{3}=1$

C．

x^'2+y^'2=1

D．

x^'2+y^'2=12

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．从5位男同学和4位女同学中选出3位同学分别担任数、语、外三科的科代表，要求选出的3位同学中男女都要有，则不同的选派方案共有（　　）

A．

210种

B．

630种

C．

420种

D．

840种

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

6．

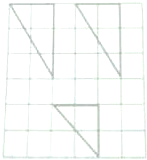如图，网格纸上小正方体的边长为1，粗实线画出的是某多面体的三视图（第一个为主视图，下面的是俯视图），则该多面体各个面的面积最大值为$3\sqrt{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

16．已知定点M（-$\sqrt{2}，0}$），N是圆C：（x-$\sqrt{2}}$）²+y²=16（C为圆心）上的动点，MN的垂直平分线与NC交于点E．
（1）求动点E的轨迹方程C₁；
（2）直线l与轨迹C₁交于P，Q两点，与抛物线C₂：x²=4y交于A，B两点，且抛物线C₂在点A，B处的切线垂直相交于S，设点S到直线l的距离为d，试问：是否存在直线l，使得d=$\sqrt{|{AB}|•|{PQ}|}$？若存在，求直线l的方程；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知在△ABC中，角A、B、C的对边分别为a、b、c，向量$\overrightarrow m$=（b，c-2a），$\overrightarrow n$=（2cosC，1），且|$\overrightarrow m$+$\overrightarrow n$|=|$\overrightarrow m$-$\overrightarrow n$|．
（I）求∠B的大小；
（II）若b=2，求△ABC面积S的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

20．在△ABC中，AB=2，AC=3，$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$，则$\overrightarrow{AD}$•$\overrightarrow{BD}$=$\frac{5}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题